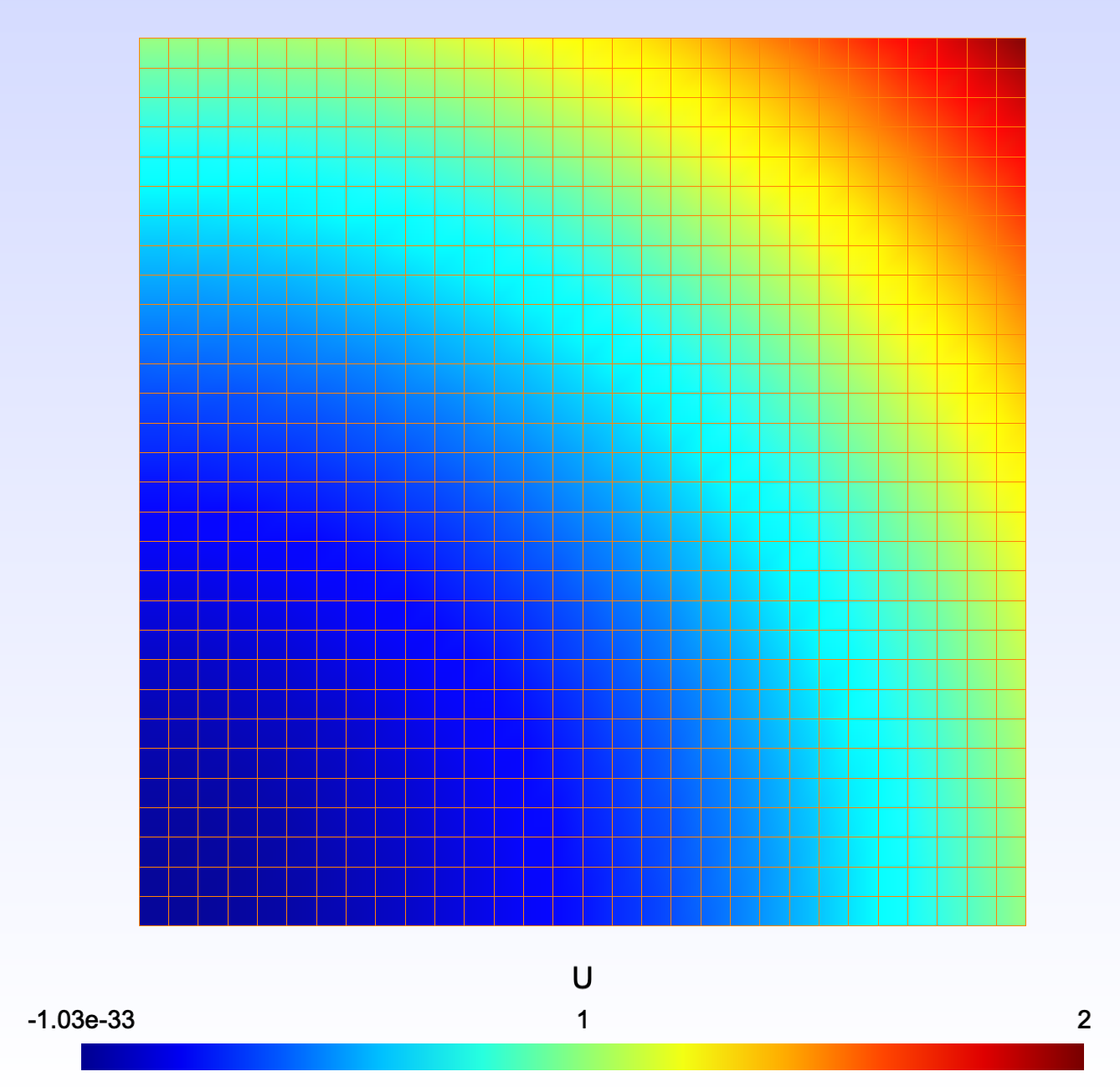
Poisson equation

The laplacian in a square is the usual starting point of PDEs.

Note

The problem is optionnally solved as non-linear in a Newton algorithm in order to be convinced of the correctness of the formulation.

Note

An analytical solution may be given as an expression to be compared with. Note that it is the same expression than the imposed value at the boundaries. It is better have them equal on that common zone …

//
//  nvi_Poisson__0.cpp
//  Navpactos-OSX9
//
//  Created by Matthieu on 08/10/2014.
//  Copyright (c) 2014 Naupacte S.A.R.L. All rights reserved.
//

#include "nvi_Poisson.h"
#include "nvi_Formulation__framework_01.h"
#include "navlib_array.h"

#include <iostream>

namespace nvi::FormulationFrameworks
{
    struct UProblem__Poisson_X2Y2 : public Formulation__framework_01
    {
        struct parameters_t
        {
            bool newton = false;
            uint degreeU = 1;
            
            NodeSpecificator dirichlet;
        };
        UProblem__Poisson_X2Y2(Processor& p, txt name, Mesh&& m, const parameters_t& pp) : Formulation__framework_01(p,name,std::move(m))
        {
            auto U = variable("U",pp.degreeU);
            
            auto points = _points_();
            auto dx     = _dx_();
            
            auto Id = identity_matrix();
            
            auto source = 4.;
            auto bc = _x*_x+_y*_y;

            auto V = dual(U);
            
            auto      v =      V (points);
            auto grad_v = grad(V)(points);
            
            auto formU  = form1(dx*source,v);

            if (pp.newton)
            {
                auto grad_u = grad(U)(points);

                formU += form1(dx*grad_u,grad_v);
            }
            auto formUU = form2(dx*Id, grad_v);
            
            assemble_in_vector(U,formU);
            assemble_in_matrix(U,formUU);
            
            analytic_solution = bc;

            add_Dirichlet("Dirichlet",U,pp.dirichlet,0,{bc});
        }
    };
}


void nvi::Poisson_0_grid2(txt output_dir)
{
    using namespace FormulationFrameworks;
    using namespace SpaceDiscretisation;
    text name = __FUNCTION__;
    
    auto processor = Processor__get (name,output_dir);

    const bool newton = true;
    const uint degreeX = 2;
    
    auto pb = UProblem__Poisson_X2Y2(processor,name,
                                     Mesh(processor,Grid2(30,30,degreeX)),
                                     {
        .newton = newton,
        .degreeU = 2,
        .dirichlet = { "X=0", "Y=0 internal", "X=1", "Y=1 internal"},
    });
    if (newton)
    {
        pb.newton_options.number_of_iterations = 5;
        pb.solve();
    }
    else
    {
        pb.line_solve();
    }
    
    pb.compare_to_solution(1.e-10, 1.e-10, 0);
    pb.save();
}

void nvi::Poisson_0_gmsh2(txt output_dir)
{
    using namespace FormulationFrameworks;
    using namespace SpaceDiscretisation;
    text name = __FUNCTION__;
    
    auto processor = Processor__get (name,output_dir);

    const bool newton = true;

    auto pb = UProblem__Poisson_X2Y2(processor,name,
                                     Mesh(processor, 2,"./tests/data/meshes/Qua-20-20-O2-cavity.msh"),
                                     {
        .newton = newton,
        .degreeU = 2,
        .dirichlet = { "left", "right", "top", "bottom"}
    });
    
    if (newton)
    {
        pb.newton_options.number_of_iterations = 5;
        pb.solve();
    }
    else
    {
        pb.line_solve();
    }

    pb.save();
}

Results