Coupled equations: Electricity x Thermics
Unknows are the electrical potential \(U\) and the temperature \(T\) or \(\theta\).

Model

The coupled system potential x temperature
A tension is applied by setting \(U=0\) on the left side and \(U=1\) on the right side. The temperature is set to 0 at these same boundaries, while a convective exchange applies elsewhere at the boundary, the external convective temperature being \(T_{\rm ext}\).
The other parameters of the problem are the material properties:
the electric conductivity \(\sigma = \sigma_0+\sigma_1 \theta\),
the thermal conductivity \(\kappa\),
the volumic thermal capacity \(c_p\) (that enables deducing temperature increase from heat production),
the exchange coefficient \(\beta\).
Here is the pseudosystem with only the volumic contributions. In red, the test functions of \(\theta\); in blue, those of \(u\).

That is a fully coupled multiphysics system of equations. We’ll see how to define the matrix and the right-hand side.
Sensitivities
Furthermore, some additional results will be provided: the derivatives of the solution with respect to some coefficients (electrical conductivity, thermal exchange coefficient). For this, the only additional need is the formulation of the right-hand side derivatives as the solver will perform the corresponding line-solves with the matrix obtained at the last Newton iteration to give the proper result (there is a negative sign in the box).
Code
/*
* nvi_Conductivity_x_Thermics.cpp
* Navpactos
*
* Created by Matthieu on 15/03/13.
* Copyright 2013 Naupacte S.A.R.L. All rights reserved.
*
*/
#include "nvi_Conductivity.h"
#include "nvi_Formulation__framework_01.h"
namespace nvi::FormulationFrameworks
{
struct Conductivity_x_thermics_0 : public Formulation__framework_01
{
struct parameters_t
{
uint degreeU = 1;
uint degreeT = 1;
NodeSpecificator dirichlet0; //! Nodes with imposed values : T=0; U=0
NodeSpecificator dirichlet1; //! Nodes with imposed values : T=0; U=1
ElementSideSpecificator exchange; //! Exchange boundary
//! Electrical conductivity: sigma = sigma0 + sigma1*T
Expr sigma0 = 4000.;
Expr sigma1 = -10.;
Expr kappa = 1.; //! Thermal conductivity
Expr cp = 1.; //! Thermal capacity
//! at exchange boundary:
Expr beta = 5.; //! Thermal exchange coefficient
Expr tme = -10.; //! External temperature
};
Conductivity_x_thermics_0(Processor& proc, txt name, Mesh&& m, const parameters_t& pp) : Formulation__framework_01(proc,name,std::move(m))
{
auto Id = identity_matrix();
//! variables U & T
auto U = variable("U", pp.degreeU);
auto T = variable("T", pp.degreeT);
//! integration points and integrand
auto points = _points_ ();
auto dx = _dx_();
//! tensors at integration points
auto x = X (points);
auto grad_u = grad(U)(points);
auto tm = T (points);
auto grad_tm = grad(T)(points);
//! test variables
auto U_ = dual(U);
auto T_ = dual(T);
//! test tensors at integration points
auto grad_u_ = grad(U_)(points);
auto tm_ = T_ (points);
auto grad_tm_ = grad(T_)(points);
//! coefficients at integration points
auto sigma0 = scalar_of_X(pp.sigma0,x);
auto sigma1 = scalar_of_X(pp.sigma1,x);
auto kappa = scalar_of_X(pp.kappa, x);
auto cp = scalar_of_X(pp.cp, x);
auto sigma = sigma0 + sigma1*tm;
//! linear and bilinear forms
auto formU = form1(dx*sigma*grad_u,grad_u_);
auto formUU = form2(dx*sigma*Id, grad_u_);
auto formT = form1(dx*kappa*grad_tm,grad_tm_) + form1(-dx/cp*sigma *pow(norm2(grad_u),2),tm_);
auto formTT = form2(dx*kappa*Id, grad_tm_) + form2(-dx/cp*sigma1*pow(norm2(grad_u),2),tm_);
auto formTU = form2(-dx*2/cp*sigma *grad_u,tm_,grad_u_);
auto formUT = form2( dx *sigma1*grad_u,grad_u_,tm_);
//! additional formulation: derivative vs sigma
auto formUs = form1( dx*tm*grad_u,grad_u_);
auto formTs = form1(-dx/cp*tm *pow(norm2(grad_u),2),tm_);
//! assembly specification in rhs vector
assemble_in_vector(U,formU);
assemble_in_vector(T,formT);
//! assembly specification in matrix
assemble_in_matrix(U,formUU);
assemble_in_matrix(T,formTT);
assemble_in_matrix(U,T,formUT);
assemble_in_matrix(T,U,formTU);
//! boundary conditions: a name is given for the lagrange multiplier variable
add_Dirichlet("Dirichlet0",U,{pp.dirichlet0});
add_Dirichlet("Dirichlet1",U,{pp.dirichlet1},{Expr(1.)});
add_Dirichlet("Dirichlet0",T,{pp.dirichlet0});
add_Dirichlet("Dirichlet1",T,{pp.dirichlet1},{Expr(0.)});
#define NV_ADDITIONAL
#ifdef NV_ADDITIONAL
//! additional formulation: derivative vs sigma
const uint iSigma = additional_vector("∂/∂σ");
assemble_in_vector(U,formUs);
assemble_in_vector(T,formTs);
//! additional formulation: derivative vs beta
const uint iBeta = additional_vector("∂/∂β");
#endif
//! thermal exchange at specified boundary
if (pp.exchange!="")
{
//! sides extraction from specification
auto s = sides(pp.exchange);
//! integration points and integrand on sides
auto local_points = s._local_reference_points_();
auto ds = s._ds_();
//! tensors at integration points
auto x = s(X) (local_points);
auto tm = s(T) (local_points);
auto tm_ = s(T_)(local_points);
//! coefficients at integration points
auto beta = scalar_of_X(pp.beta,x);
auto tme = scalar_of_X(pp.tme, x);
//! linear and bilinear forms
auto formT = form1(-ds*beta*(tm-tme),tm_);
auto formTT = form2(-ds*beta, tm_);
auto formTb = form1(-ds* (tm-tme),tm_);
//! assembly specification in rhs vector and matrix
set_actual_vector(0); //! last current vector index was iBeta
s.assemble_in_vector(T,formT);
s.assemble_in_matrix(T,formTT);
#ifdef NV_ADDITIONAL
//! additional formulation: derivative vs beta
set_actual_vector(iBeta);
s.assemble_in_vector(T,formTb);
#endif
}
}
};
}
// Calling the model with the parameters
void nvi::Conductivity_x_Thermics_0_gmsh2(txt output_dir)
{
using namespace SpaceDiscretisation;
using namespace FormulationFrameworks;
text name = __FUNCTION__;
//! output and hierarchical log processor
auto processor = Processor__get (name,output_dir);
auto meshname = "./tests/data/meshes/cylindre_O1.msh";
auto pb = Conductivity_x_thermics_0(processor,name,
Mesh(processor,2,meshname),
{
.degreeU = 1,
.degreeT = 1,
.dirichlet0 = "inflow",
.dirichlet1 = "outflow",
.exchange = "noslip",
.sigma0 = 4000.,
.sigma1 = -10.,
.kappa = 1.,
.cp = 1.,
.beta = 5.,
.tme = -10.
});
//! some options for Newton algorithm
pb.newton_options.number_of_primal_variables = 2; // U and T; others are Lagrange's multipliers
pb.newton_options.number_of_iterations = 15;
pb.solve();
pb.save();
}
Results
The results are shown for the electrical potential and its sensitivities:
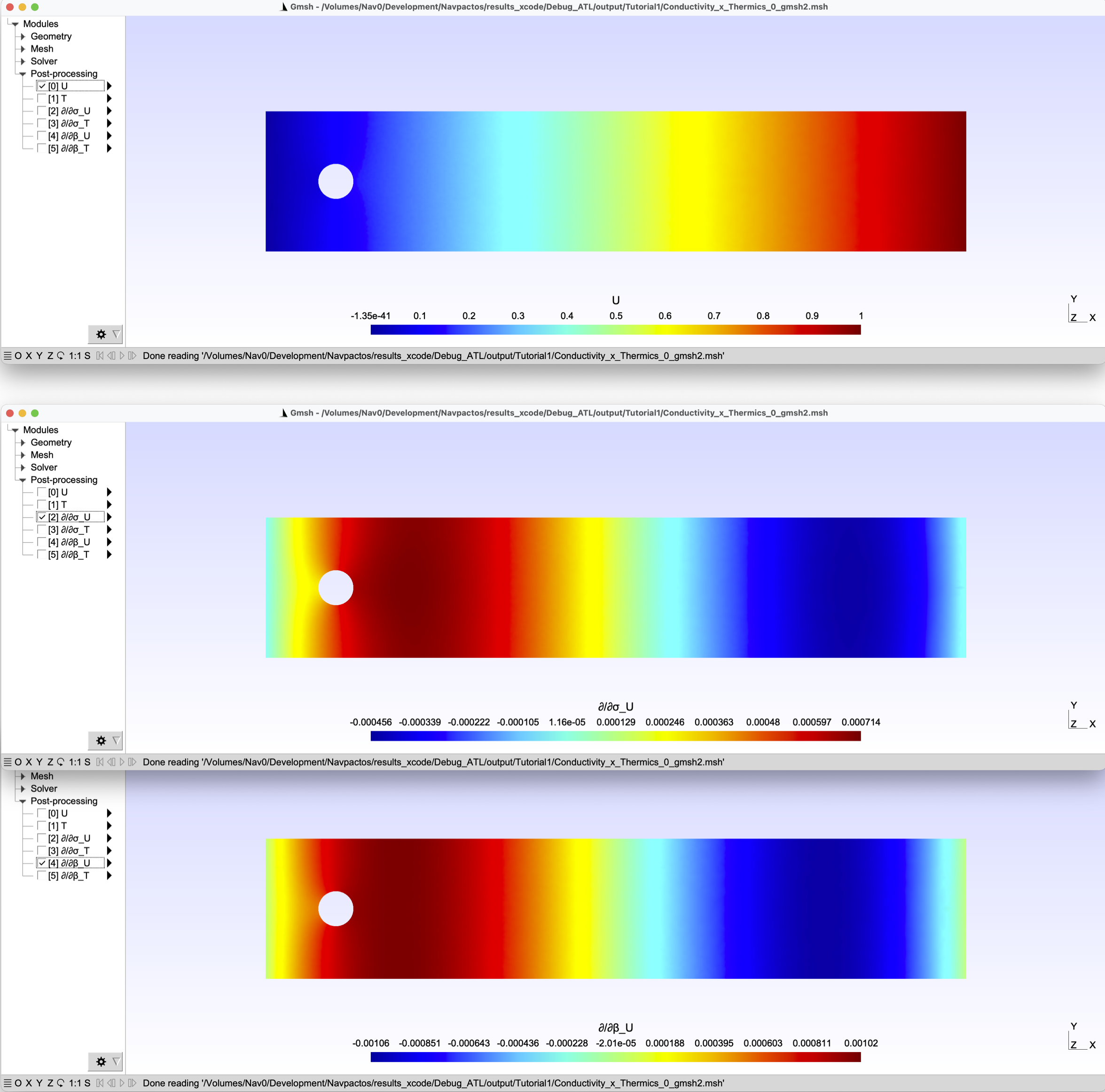
“U, ∂U/∂σ1, ∂U/∂ß”
and for the temperature and its sensitivities:
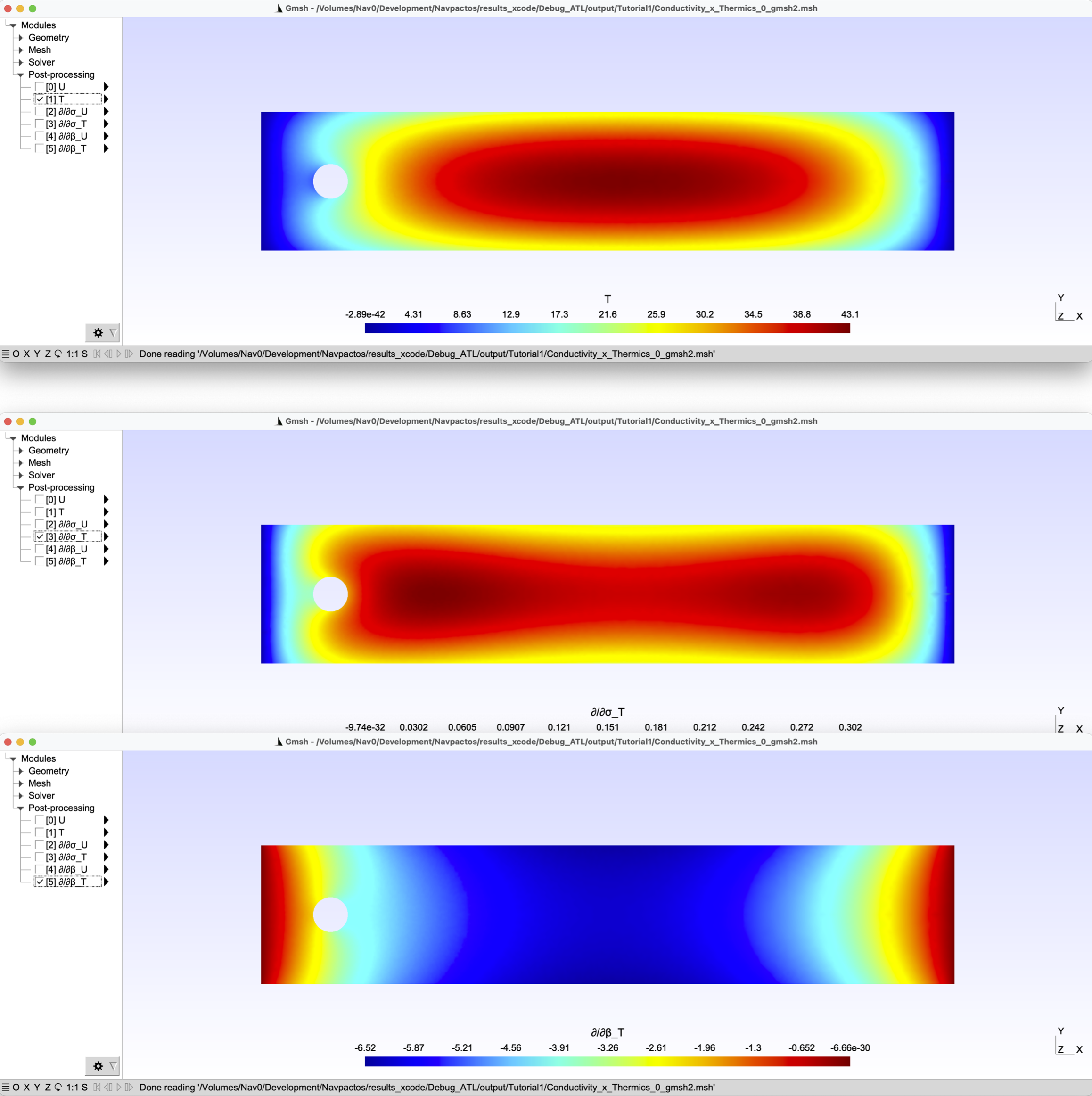
“T, ∂T/∂σ1, ∂T/∂ß”
Log file
1 - Reading "" mesh from file ./tests/data/meshes/cylindre_O1.msh
. 1 - Gmsh: reading mesh
. . 1 - Reading section $MeshFormat
. . 2 - Reading section $PhysicalNames
. . 3 - Reading section $Nodes
. . 4 - Reading section $Elements
1 1 * Gmsh: reading mesh : logs: 0, time: 9.84 ms (cpu: 30 ms)
. 2 - Post reading
. . 1 - Element groups
. . 2 - Degree analysis
1 2 * Post reading: logs: 0, time: 391 us (cpu: 0 ms)
. 3 - Gmsh: FeConnectivity from all GmshMesh elements of dimension 2
. . 1 - Gmsh: FeConnectivity from GmshMesh elements; n=19928
1 3 * Gmsh: FeConnectivity from all GmshMesh elements of dimension 2: logs: 0, time: 1.89 ms (cpu: 20 ms)
1 * Reading "" mesh from file ./tests/data/meshes/cylindre_O1.msh: logs: 0, time: 14.3 ms (cpu: 70 ms)
2 - Creating variable U: [], degree=1
3 - Creating variable T: [], degree=1
4 - Extracting sides
. 1 - Gmsh: FeConnectivity from all GmshMesh elements of dimension 2
. . 1 - Gmsh: FeConnectivity from GmshMesh elements; n=19928
4 1 # Gmsh: FeConnectivity from all GmshMesh elements of dimension 2: logs: 1, time: 498 us (cpu: 10 ms)
. 2 - Gmsh: FeConnectivity from GmshMesh elements; n=610
4 # Extracting sides: logs: 1, time: 4.45 ms (cpu: 70 ms)
5 - Building
. 1 - Identifying unknown variables
. 2 - Building system
. . 1 - Matrix formulations
. . 2 - Matrix formulations
. . 3 - Matrix formulations
. . 4 - Matrix formulations
. . 5 - Matrix formulations
. . 6 - Vector formulations
. . 7 - Vector formulations
. . 8 - Vector formulations
. . 9 - Dirichlet conditions
. . 10 - Dirichlet conditions
. . 11 - Dirichlet conditions
. . 12 - Dirichlet conditions
. . 13 - Building additional vectors
. . . 1 - Vector formulations
. . . 2 - Vector formulations
. . . 3 - Vector formulations
5 2 13 * Building additional vectors: logs: 0, time: 211 us (cpu: 0 ms)
5 2 * Building system: logs: 0, time: 1.95 ms (cpu: 30 ms)
5 # Building: logs: 1, time: 2.01 ms (cpu: 30 ms)
6 - System instantiation
>> symmetry_respect: 0; hermitian_kind 1
$chrono SmartSystem_instantiation: 85.8 ms (cpu: 1.32 s)
7 - Newton initialization
8 - Newton iterations Time[1] = 1
===========================================================
NEWTON : ITERATION 1
===========================================================
|| rhsU0 || = 0 0
|| rhsU1 || = 0.416667 9.10753
|| rhsU || = 0.416667 9.10753
|| rhsL2 || = 0 0
|| rhsL3 || = 1 6.245
|| rhsL4 || = 0 0
|| rhsL5 || = 0 0
|| rhsL || = 1 11.043
|| lhsU0 || = 1 46.3304
|| lhsU1 || = 9.8455 857.486
|| lhsU || = 9.8455 858.736
|| lhsL2 || = 45.6737 182.042
|| lhsL3 || = 20.6272 126.315
|| lhsL4 || = 1.60893 4.71025
|| lhsL5 || = 0.896591 3.064
|| lhsL || = 45.6737 886.879
---------------- ITERATION 1 TIMES ----------------------
$chrono assembly: 5.94 ms (cpu: 80 ms)
$chrono analysis: 35.8 ms (cpu: 550 ms)
$chrono factorisation: 9.4 ms (cpu: 130 ms)
$chrono line_solve: 2.92 ms (cpu: 50 ms)
$chrono Newton iteration: 54.6 ms (cpu: 820 ms)
===========================================================
NEWTON : ITERATION 2
===========================================================
|| rhsU0 || = 0.127534 0.941117
|| rhsU1 || = 0.932605 11.291
|| rhsU || = 0.932605 11.3302
|| rhsL2 || = 5.50347e-26 1.23039e-25
|| rhsL3 || = 0 0
|| rhsL4 || = 2.50754e-28 5.78141e-28
|| rhsL5 || = 1.19708e-28 3.77935e-28
|| rhsL || = 0.932605 11.3302
|| lhsU0 || = 0.00657742 0.470183
|| lhsU1 || = 52.9409 3683.54
|| lhsU || = 52.9409 3683.54
|| lhsL2 || = 3.11306 12.6729
|| lhsL3 || = 1.67994 8.80648
|| lhsL4 || = 3.91076 15.7042
|| lhsL5 || = 2.4645 12.9868
|| lhsL || = 52.9409 3683.63
lhsU / lhsU0 = 5.37716
lhsL / lhsL0 = 1.15911
---------------- ITERATION 2 TIMES ----------------------
$chrono assembly: 4.51 ms (cpu: 60 ms)
$chrono analysis: 36.2 ms (cpu: 570 ms)
$chrono factorisation: 8.39 ms (cpu: 120 ms)
$chrono line_solve: 2.69 ms (cpu: 50 ms)
$chrono Newton iteration: 52.2 ms (cpu: 810 ms)
===========================================================
NEWTON : ITERATION 3
===========================================================
|| rhsU0 || = 0.023025 0.193602
|| rhsU1 || = 0.0040697 0.0424047
|| rhsU || = 0.023025 0.198192
|| rhsL2 || = 2.57507e-27 8.56388e-27
|| rhsL3 || = 0 0
|| rhsL4 || = 1.73113e-27 6.1067e-27
|| rhsL5 || = 7.4408e-28 3.46139e-27
|| rhsL || = 0.023025 0.198192
rhsU / rhsU0 = 0.0246889
rhsL / rhsL0 = 0.023025
|| lhsU0 || = 0.000462342 0.0314277
|| lhsU1 || = 0.0713744 4.85309
|| lhsU || = 0.0713744 4.85319
|| lhsL2 || = 0.0372317 0.133971
|| lhsL3 || = 0.018047 0.0943742
|| lhsL4 || = 0.00205879 0.00790553
|| lhsL5 || = 0.000516078 0.00281346
|| lhsL || = 0.0713744 4.85596
lhsU / lhsU0 = 0.00724944
lhsL / lhsL0 = 0.0015627
---------------- ITERATION 3 TIMES ----------------------
$chrono assembly: 4.31 ms (cpu: 60 ms)
$chrono analysis: 36.9 ms (cpu: 580 ms)
$chrono factorisation: 8.15 ms (cpu: 120 ms)
$chrono line_solve: 2.62 ms (cpu: 40 ms)
$chrono Newton iteration: 52.5 ms (cpu: 810 ms)
===========================================================
NEWTON : ITERATION 4
===========================================================
|| rhsU0 || = 2.94716e-06 2.10945e-05
|| rhsU1 || = 4.74289e-06 3.59851e-05
|| rhsU || = 4.74289e-06 4.17122e-05
|| rhsL2 || = 4.06494e-28 1.56715e-27
|| rhsL3 || = 0 0
|| rhsL4 || = 6.09196e-29 2.37815e-28
|| rhsL5 || = 1.43193e-29 7.51445e-29
|| rhsL || = 4.74289e-06 4.17122e-05
rhsU / rhsU0 = 5.08563e-06
rhsL / rhsL0 = 4.74289e-06
|| lhsU0 || = 3.67033e-08 2.12532e-06
|| lhsU1 || = 0.000159405 0.00922877
|| lhsU || = 0.000159405 0.00922877
|| lhsL2 || = 6.72783e-06 2.71509e-05
|| lhsL3 || = 3.98436e-06 1.89008e-05
|| lhsL4 || = 1.58849e-05 6.39618e-05
|| lhsL5 || = 7.21505e-06 3.95675e-05
|| lhsL || = 0.000159405 0.00922914
lhsU / lhsU0 = 1.61906e-05
lhsL / lhsL0 = 3.49007e-06
---------------- ITERATION 4 TIMES ----------------------
$chrono assembly: 4.54 ms (cpu: 60 ms)
$chrono analysis: 35.5 ms (cpu: 550 ms)
$chrono factorisation: 7.83 ms (cpu: 120 ms)
$chrono line_solve: 2.77 ms (cpu: 50 ms)
$chrono Newton iteration: 51.1 ms (cpu: 800 ms)
===========================================================
NEWTON : ITERATION 5
===========================================================
|| rhsU0 || = 1.29496e-12 2.85444e-11
|| rhsU1 || = 9.67427e-10 4.21836e-09
|| rhsU || = 9.67427e-10 4.21845e-09
|| rhsL2 || = 1.73346e-32 5.76883e-32
|| rhsL3 || = 0 0
|| rhsL4 || = 2.24289e-33 5.23235e-33
|| rhsL5 || = 5.48007e-34 1.53225e-33
|| rhsL || = 9.67427e-10 4.21845e-09
rhsU / rhsU0 = 1.03734e-09
rhsL / rhsL0 = 9.67427e-10
|| lhsU0 || = 2.44078e-13 1.22296e-11
|| lhsU1 || = 1.84168e-09 4.02169e-08
|| lhsU || = 1.84168e-09 4.02169e-08
|| lhsL2 || = 5.96002e-11 2.02166e-10
|| lhsL3 || = 3.51131e-11 1.43858e-10
|| lhsL4 || = 3.42888e-10 6.97343e-10
|| lhsL5 || = 7.06601e-10 8.54158e-10
|| lhsL || = 1.84168e-09 4.02328e-08
lhsU / lhsU0 = 1.87058e-10
lhsL / lhsL0 = 4.03226e-11
---------------- ITERATION 5 TIMES ----------------------
$chrono assembly: 4.67 ms (cpu: 70 ms)
$chrono analysis: 36.7 ms (cpu: 570 ms)
$chrono factorisation: 7.21 ms (cpu: 110 ms)
$chrono line_solve: 2.81 ms (cpu: 50 ms)
$chrono Newton iteration: 51.9 ms (cpu: 810 ms)
===========================================================
NEWTON : ITERATION 6
===========================================================
|| rhsU0 || = 1.25588e-12 2.86434e-11
|| rhsU1 || = 8.2212e-14 6.24541e-13
|| rhsU || = 1.25588e-12 2.86502e-11
|| rhsL2 || = 7.99437e-38 2.9549e-37
|| rhsL3 || = 0 0
|| rhsL4 || = 5.21404e-38 1.5504e-37
|| rhsL5 || = 1.39362e-38 4.25594e-38
|| rhsL || = 1.25588e-12 2.86502e-11
rhsU / rhsU0 = 1.34664e-12
rhsL / rhsL0 = 1.25588e-12
|| lhsU0 || = 1.18992e-16 4.87457e-15
|| lhsU1 || = 1.02767e-13 1.02462e-12
|| lhsU || = 1.02767e-13 1.02463e-12
|| lhsL2 || = 2.91932e-14 5.98096e-14
|| lhsL3 || = 8.69704e-15 2.69142e-14
|| lhsL4 || = 1.1189e-14 1.80651e-14
|| lhsL5 || = 2.12833e-14 2.27402e-14
|| lhsL || = 1.02767e-13 1.02714e-12
lhsU / lhsU0 = 1.04379e-14
lhsL / lhsL0 = 2.25002e-15
---------------- ITERATION 6 TIMES ----------------------
$chrono assembly: 4.41 ms (cpu: 70 ms)
$chrono analysis: 36.9 ms (cpu: 570 ms)
$chrono factorisation: 8.41 ms (cpu: 130 ms)
$chrono line_solve: 2.64 ms (cpu: 40 ms)
$chrono Newton iteration: 52.8 ms (cpu: 810 ms)
===========================================================
===========================================================
===========================================================
===========================================================
===========================================================
*** Newton convergence in 6 iterations. STOP. ***
===========================================================
===========================================================
===========================================================
$chrono assembly <mean>: 4.73 ms (cpu: 60 ms)
$chrono analysis <mean>: 36.3 ms (cpu: 560 ms)
$chrono factorisation <mean>: 8.23 ms (cpu: 120 ms)
$chrono line_solve <mean>: 2.74 ms (cpu: 40 ms)
$chrono update <mean>: 323 us (cpu: 0 ms)
$chrono Newton iteration <mean>: 52.5 ms (cpu: 810 ms)
9 - Additional rhs vectors
10 - Writing mesh solution: Conductivity_x_Thermics_0_gmsh2