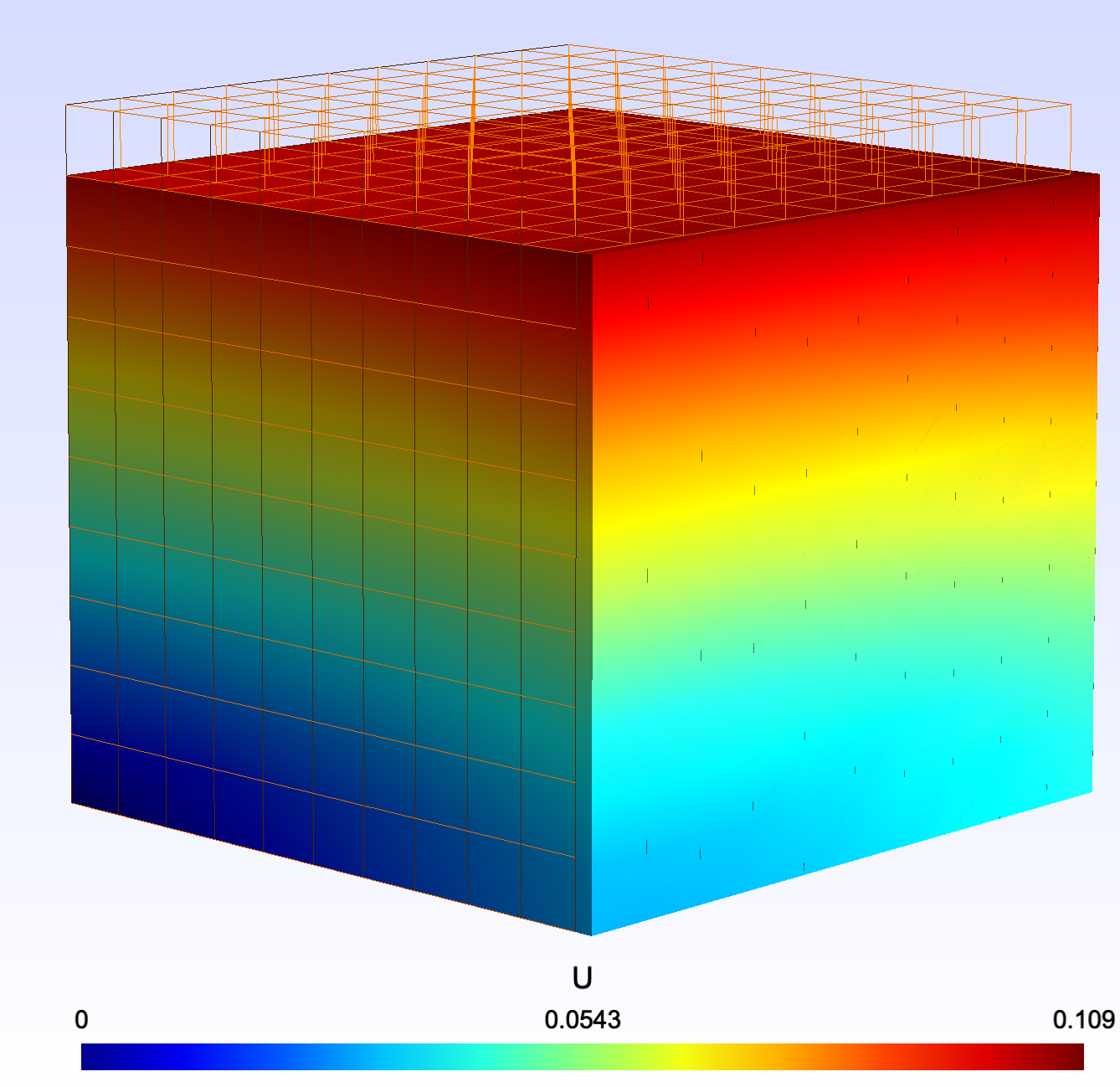
Linear Elasticity

Only the constant stiffness matrix WCC is needed for the formulation.

//
//  nvi_LinearElasticity__form__grid3.cpp
//  Navpactos-OSX9
//
//  Created by Matthieu on 08/10/2014.
//  Copyright (c) 2014 Naupacte S.A.R.L. All rights reserved.
//

#include "nvi_LinearElasticity.h"
#include "nvi_Formulation__framework_01.h"
#include "nvi_Material.h"
#include "nvi_Material_FunctionX_Factory.h"

#include <iostream>

namespace nvi::FormulationFrameworks
{
    using namespace Material;
    struct UProblem__LinearElasticity0 : public Formulation__framework_01
    {
        UProblem__LinearElasticity0(Processor& p, txt name, Mesh&& m, uint degreeU) : Formulation__framework_01(p,name,std::move(m))
        {
            auto U = variable("U",3,degreeU);
            
            auto points = _points_ ();
            auto dx     = _dx_();
                                                
            auto V = dual(U);
            auto Dv = D(V)(points);
                        
            // stiffness
            auto WCC = WCC__E_nu(1.e5,0.3);
            
            auto formUU = form2(dx*WCC,Dv+transpose(Dv)); // = form2(dx* 4*WCC,Dv)

            assemble_in_matrix(U,formUU);
            
            // Imposed dofs

            // The bottom nodes remain on their plane
            add_Dirichlet("Dirichlet",U,{"Z=0"},       2, 0.);
            
            // The top nodes are imposed a vertical displacement
            const double deltaZ = -0.1; // could be an Expr of X.
            add_Dirichlet("Dirichlet",U,{"Z=1"},       2, deltaZ);
            
            // Prevent the rigid body motion by blocking node O and keeping node (1,0,0) on its axis
            add_Dirichlet("Dirichlet",U,{"Origin"},    0, 0.);
            add_Dirichlet("Dirichlet",U,{"Origin"},    1, 0.);
            add_Dirichlet("Dirichlet",U,{"Axis X end"},1, 0.);
        }
    };
}

void nvi::LinearElasticity_0(txt output_dir)
{
    using namespace SpaceDiscretisation;
    using namespace FormulationFrameworks;
    text name = __FUNCTION__;
    
    auto processor = Processor__get (name,output_dir);
    
    const uint degreeX = 1;
    const uint degreeU = 1;
    
    uint ne1 = 10;
    uint ne2 = 10;
    uint ne3 = 10;
    
    auto pb = UProblem__LinearElasticity0(processor,name,Mesh(processor,Grid3(ne1,ne2,ne3,degreeX)),degreeU);
        
    pb.line_solve();
    
    pb.save();
    
}

Linear Elasticity solved as non-linear

We solve the same problem but this time considering it as non-linear. We need to give the formulation of the residual, even it is null. The Newton algorithm shall convice us it is so.

//
//  nvi_LinearElasticity__form__grid3.cpp
//  Navpactos-OSX9
//
//  Created by Matthieu on 08/10/2014.
//  Copyright (c) 2014 Naupacte S.A.R.L. All rights reserved.
//

#include "nvi_LinearElasticity.h"
#include "nvi_Formulation__framework_01.h"
#include "nvi_Material.h"
#include "nvi_Material_FunctionX_Factory.h"

#include <iostream>

namespace nvi::FormulationFrameworks
{
    using namespace Material;
    struct UProblem__LinearElasticity0__as_nonlinear : public Formulation__framework_01
    {
        UProblem__LinearElasticity0__as_nonlinear(Processor& p, txt name, Mesh&& m, uint degreeU) : Formulation__framework_01(p,name,std::move(m))
        {
            auto U = variable("U",3,degreeU);
            
            auto points = _points_ ();
            auto dx     = _dx_();
            
            auto x  =   X (points);
            auto Du = D(U)(points);
            
            auto Id = identity_matrix();
            
            auto materialData = hooke_E_nu(1.e5,0.3); // the coefficients could be expressions (Expr) of X
            
            auto V = dual(U);
            auto Dv = D(V)(points);
            
            // C is the linearized strain deformation
            auto C = Id+Du+transpose(Du);
            
            // We get the energy, stress, and stiffness
            auto [W,WC,WCC] = energyC_tensors(C,materialData);
            
            // Here come the variations of the total energy on the element (Wtot = form0(dx*W))
            // formU  : elementary vector
            // formUU : elementary matrix
            auto formU  = form1(dx*WC, Dv+transpose(Dv)); // = form1(dx* 2*WC, Dv);
            auto formUU = form2(dx*WCC,Dv+transpose(Dv)); // = form2(dx* 4*WCC,Dv);

            // Define rhs and matrix
            // with the assembly of the elementary vector and matrix using the nodes of U
            assemble_in_vector(U,formU); // not necessary as it the problem is linear but allow to check its correctness
            assemble_in_matrix(U,formUU);
            
            // Imposed dofs

            // The bottom nodes remain on their plane
            add_Dirichlet("Dirichlet",U,{"Z=0"},       2, 0.);
            
            // The top nodes are imposed a vertical displacement
            const double deltaZ = -0.1; // could be an Expr of X.
            add_Dirichlet("Dirichlet",U,{"Z=1"},       2, deltaZ);
            
            // Prevent the rigid body motion by blocking node O and keeping node (1,0,0) on its axis
            add_Dirichlet("Dirichlet",U,{"Origin"},    0, 0.);
            add_Dirichlet("Dirichlet",U,{"Origin"},    1, 0.);
            add_Dirichlet("Dirichlet",U,{"Axis X end"},1, 0.);
        }
    };
}

void nvi::LinearElasticity0__as_nonlinear(txt output_dir)
{
    using namespace SpaceDiscretisation;
    using namespace FormulationFrameworks;
    text name = __FUNCTION__;
    
    auto processor = Processor__get (name,output_dir);
    
    const uint degreeX = 1;
    const uint degreeU = 1;
    
    uint ne1 = 10;
    uint ne2 = 10;
    uint ne3 = 10;
    
    auto pb = UProblem__LinearElasticity0__as_nonlinear(processor,name,Mesh(processor,Grid3(ne1,ne2,ne3,degreeX)),degreeU);
    
    pb.newton_options.number_of_iterations = 4;
    pb.newton_options.eps_r                = 1.e-10;
    
    pb.solve();
    
    pb.save();
    
}

Results