Hyperelastic structure
Incompressible
The \(p(\det(F)-1)\) term in the lagrangian must be derivated with respect to \(U\) (via \(F\)) and \(P\). See as well the Stokes equation that deals with the incompressibility. The matrix has several blocks: the diagonal energy part, the extradiagonal incompressibility block and the Dirichlet parts:
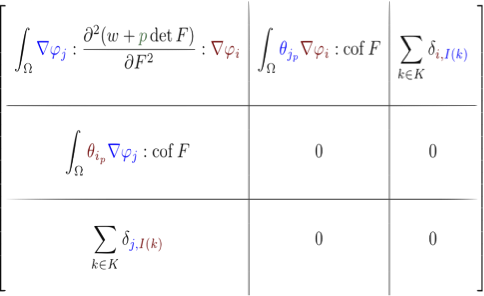
The finite element is a full degree-2 lagrange element with 27 nodes (« HEXA 27Q2 »), with a 27-point integration scheme, which implies some half MFlops per element.
//
// nvi_IncompressibleHyperElasticity_0_grid3.cpp
// Navpactos-OSX9
//
// Created by Matthieu on 08/10/2014.
// Copyright (c) 2014 Naupacte S.A.R.L. All rights reserved.
//
#include "nvi_IncompressibleHyperElasticity.h"
#include "nvi_Formulation__framework_01.h"
#include "nvi_Material.h"
#include "nvi_Material_FunctionX_Factory.h"
#include <iostream>
namespace nvi::FormulationFrameworks
{
using namespace Material;
struct UProblem__IncompressibleHyperElasticity_0 : public Formulation__framework_01
{
UProblem__IncompressibleHyperElasticity_0(Processor& proc, txt name, Mesh&& m, uint degreeU, int degreeP) : Formulation__framework_01(proc,name,std::move(m))
{
auto U = variable("U",3,degreeU);
auto P = variable("P",degreeP);
auto points = _points_ ();
auto dx = _dx_();
auto x = X(points);
auto u = U(points);
auto p = P(points);
auto DuDx = D(U)(points);
auto DpDx = D(P)(points);
auto I = identity_matrix();
auto F = I + DuDx;
auto materialData = signorini_E_nu_K(1.e5,0.3, 0.);
auto [W,WF,WFF] = energyF_tensors(F,materialData,Geometry::Invariants::ISOCHORIC_MULTIPLICATIVE);
auto U_ = dual(U);
auto P_ = dual(P);
auto v = U_ (points);
auto q = P_ (points);
auto Dv = D(U_)(points);
auto formU = form1(dx* (WF + p* cof(F)),Dv);
auto formUU = form2(dx* (WFF + p*d2det(F)),Dv);
auto formP = form1(dx* (det(F)-1), q);
auto formUP = form2(dx* cof(F), Dv,q);
assemble_in_vector(U,formU);
assemble_in_vector(P,formP);
assemble_in_matrix(U,formUU);
assemble_in_matrix(U,P,formUP,symmetric_counter_part_);
const Expr deltaZ = -0.1;
add_Dirichlet("Dirichlet",U,{"Z=0"},2);
add_Dirichlet("Dirichlet",U,{"Z=1"},2,deltaZ);
add_Dirichlet("Dirichlet",U,{"Origin"},0);
add_Dirichlet("Dirichlet",U,{"Origin"},1);
add_Dirichlet("Dirichlet",U,{"Axis X end"},1);
}
};
}
void nvi::IncompressibleHyperElasticity_0_grid3(txt output_dir)
{
using namespace FormulationFrameworks;
using namespace SpaceDiscretisation;
text name = __FUNCTION__;
auto processor = Processor__get (name,output_dir);
uint degreeU;
int degreeP;
int testcase = 1;
switch (testcase)
{
case 0: degreeU = 1; degreeP = 0; break; // Q1 P0
case 1: degreeU = 2; degreeP = 1; break; // Q2 P1D
case 2: degreeU = 2; degreeP = -1; break; // Q2 Q1
}
uint degreeX = degreeU;
uint ne1 = 10;
uint ne2 = 10;
uint ne3 = 10;
auto pb = UProblem__IncompressibleHyperElasticity_0,name,Mesh(processor, Grid3(ne1,ne2,ne3,degreeX)),degreeU,degreeP);
pb.newton_options.number_of_iterations = 5;
pb.solve();
pb.save();
}
Result
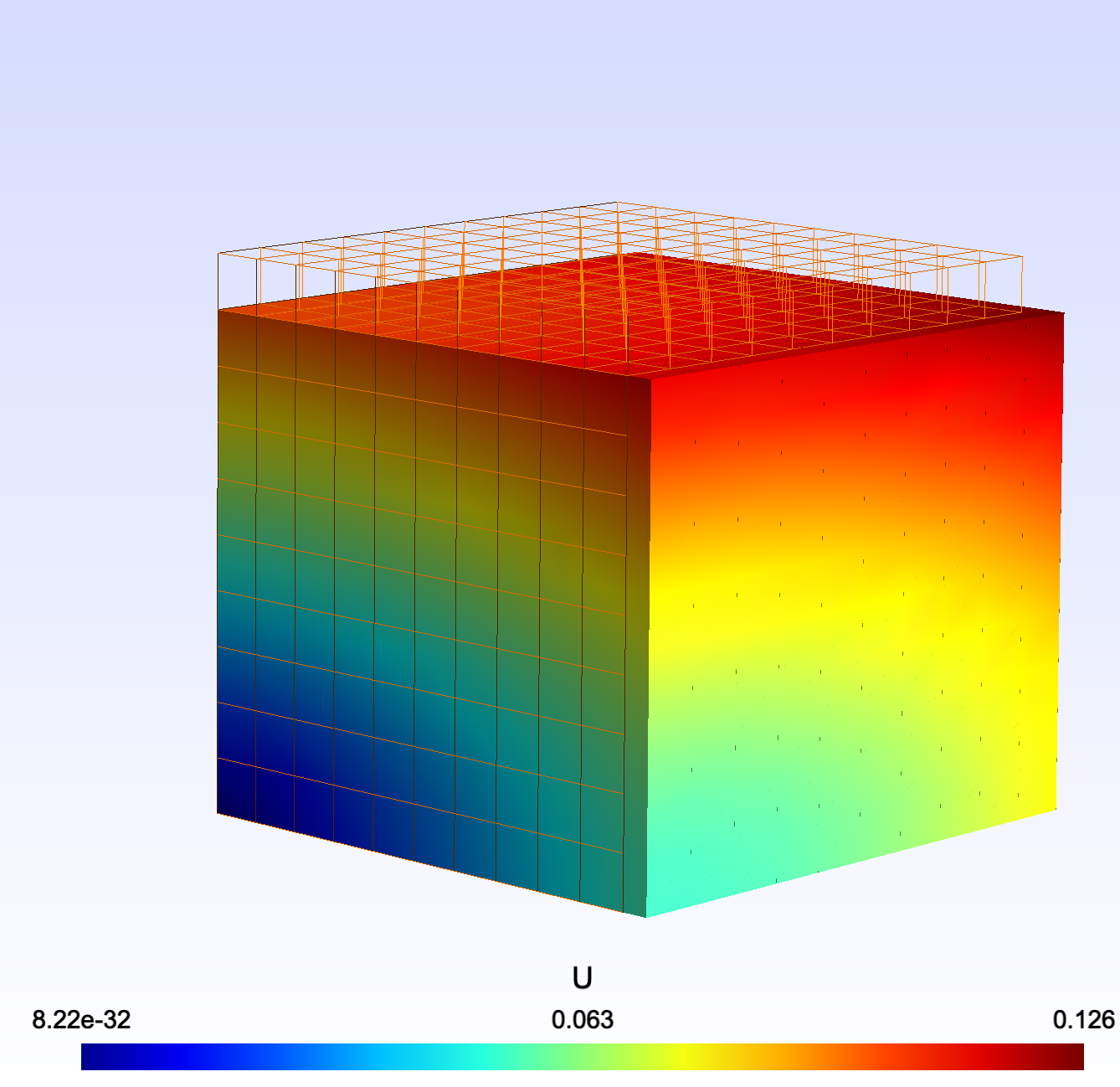
Multimaterial
The structure is divided vertically in three parts. The middle is a less stiff material. We present one way to specify the sub-domains via an ElementSpecificator. It could take a sub-domain name but here a range of elements is given.
//
// nvi_HyperElasticity__form__grid3.cpp
// Navpactos-OSX9
//
// Created by Matthieu on 08/10/2014.
// Copyright (c) 2014 Naupacte S.A.R.L. All rights reserved.
//
#include "nvi_HyperElasticity.h"
#include "nvi_Formulation__framework_01.h"
#include "nvi_Material.h"
#include "nvi_Material_FunctionX_Factory.h"
#include "nvi_Tensor_FunctionN_Factory.h"
#include "nvi_Tensor_Tools.h"
#include "navlib_array.h"
#include "navlib_array_print.h"
#include <iostream>
namespace nvi::FormulationFrameworks
{
using namespace Material;
struct UProblem__HyperElasticity_multimat_0 : public Formulation__framework_01
{
UProblem__HyperElasticity_multimat_0(Processor& p, txt name, Mesh&& m, uint degreeU) : Formulation__framework_01(p,name,std::move(m))
{
const uint dim = 3;
auto U = variable ("U", dim, degreeU);
auto V = dual(U);
U.dofs().print();
auto hooke1 = hooke_E_nu (1.e10,0.3);
auto hooke2 = hooke_E_nu (1.e9, 0.3);
struct LawDomain
{
Material::Data<decimal_t> law;
ElementSpecificator<RDIM> elements;
};
auto lawDomains =
{
LawDomain { hooke1, ElementSpecificator<RDIM>( 0,150) }, // all the elements in [0,150[
LawDomain { hooke2, ElementSpecificator<RDIM>(150,300) }, // ...
LawDomain { hooke1, ElementSpecificator<RDIM>(300,450) }, // ...
};
for (auto& [material_law,elements_spec] : lawDomains)
{
auto e = elements(elements_spec);
auto points = e._global_reference_points_();
auto dx = e._dx_();
auto I = identity_matrix();
auto x = X(points);
auto u = U(points);
auto DuDx = D(U)(points);
// Next, we choose the transposed F. But the material being isotropic, it does not matter...
// ... if we care using DvDx in formU
auto F = I + DuDx;
auto [W,WF,WFF] = energyF_tensors(F,material_law);
auto DvDx = D(V)(points); // consistent as the variation of F
auto formU = form1(dx* WF, DvDx);
auto formUU = form2(dx* WFF,DvDx);
// the assembly is made via object e to manage the right numerotation
e.assemble_in_vector(U,formU);
e.assemble_in_matrix(U,formUU);
}
const double deltaZ = -0.05;
// As no component is specified, the three components receive an imposed value (0 by default)
add_Dirichlet("Dirichlet",U,{"Z=0"});
add_Dirichlet("Dirichlet",U,{"Z=1"}, {{},{},deltaZ});
}
};
}
void nvi::HyperElasticity_multimat_0(txt output_dir)
{
using namespace SpaceDiscretisation;
using namespace FormulationFrameworks;
text name = __FUNCTION__;
auto processor = Processor__get (name,output_dir);
const uint degreeX = 2;
const uint degreeU = 2;
uint ne1 = 5;
uint ne2 = 5;
uint ne3 = 18;
auto pb = UProblem__HyperElasticity_multimat_0(processor,name,Mesh(processor,Grid3(ne1,ne2,ne3,degreeX)),degreeU);
pb.newton_options.number_of_iterations = 20;
pb.newton_options.eps_r = 1.e-10;
pb.solve();
pb.save();
}
Result
Log file
The assembly (computation of the elementary matrix and the elementary vector, and addition into a CSR matrix and a right-hand side) requires 20 ms for 450 elements with 8 cores - 16 threads. It means a speed of about 0.5 GFlops per second and per thread for 16 concurrent threads.
1 - Creating variable U: [3], degree=2
2 - Extracting elements
3 - Extracting elements
4 - Extracting elements
5 - Building
. 1 - Identifying unknown variables
. 2 - Building system
. . 1 - Vector formulations
. . 2 - Vector formulations
. . 3 - Vector formulations
. . 4 - Matrix formulations
. . 5 - Matrix formulations
. . 6 - Matrix formulations
. . 7 - Dirichlet conditions
. . 8 - Dirichlet conditions
. . 9 - Dirichlet conditions
. . 10 - Dirichlet conditions
. . 11 - Dirichlet conditions
. . 12 - Dirichlet conditions
5 2 * Building system: logs: 0, time: 1.41 ms (cpu: 20 ms)
5 * Building: logs: 0, time: 1.47 ms (cpu: 20 ms)
6 - System instantiation
>> symmetry_respect: 1; hermitian_kind 3
$chrono SmartSystem_instantiation: 76.6 ms (cpu: 1.2 s)
7 - Newton initialization
8 - Newton iterations Time[1] = 1
===========================================================
NEWTON : ITERATION 1
===========================================================
|| matrix || = 1.53519e+10 5.5128e+11
|| rhsU || = 1.15409e-07 1.32013e-06
|| rhsL1 || = 0 0
|| rhsL2 || = 0 0
|| rhsL3 || = 0 0
|| rhsL4 || = 0 0
|| rhsL5 || = 0 0
|| rhsL6 || = 0.05 0.55
|| rhsL || = 0.05 0.55
|| lhsU || = 0.05 2.16463
|| lhsL1 || = 509155 2.34359e+06
|| lhsL2 || = 509155 2.34359e+06
|| lhsL3 || = 2.98835e+06 1.47765e+07
|| lhsL4 || = 509155 2.34359e+06
|| lhsL5 || = 509155 2.34359e+06
|| lhsL6 || = 2.98835e+06 1.47765e+07
|| lhsL || = 2.98835e+06 2.14163e+07
---------------- ITERATION 1 TIMES ----------------------
$chrono assembly: 23.4 ms (cpu: 370 ms)
$chrono analysis: 181 ms (cpu: 2.82 s)
$chrono factorisation: 37.3 ms (cpu: 420 ms)
$chrono line_solve: 2.57 ms (cpu: 20 ms)
$chrono Newton iteration: 245 ms (cpu: 3.64 s)
===========================================================
NEWTON : ITERATION 2
===========================================================
|| matrix || = 1.49916e+10 5.32224e+11
|| rhsU || = 380171 3.38553e+06
|| rhsL1 || = 4.03877e-19 9.76287e-19
|| rhsL2 || = 3.24418e-19 9.47982e-19
|| rhsL3 || = 5.71369e-19 2.03948e-18
|| rhsL4 || = 2.22756e-17 5.64254e-17
|| rhsL5 || = 4.08925e-17 6.5052e-17
|| rhsL6 || = 4.85723e-17 1.98457e-16
|| rhsL || = 3.38553e+06 2.16349e-16
|| lhsU || = 0.00131026 0.044556
|| lhsL1 || = 106610 508881
|| lhsL2 || = 106610 508881
|| lhsL3 || = 456445 2.59871e+06
|| lhsL4 || = 106610 508881
|| lhsL5 || = 106610 508881
|| lhsL6 || = 456445 2.59871e+06
|| lhsL || = 456445 3.81345e+06
lhsU / lhsU0 = 0.0262051
lhsL / lhsL0 = 0.152742
---------------- ITERATION 2 TIMES ----------------------
$chrono assembly: 24 ms (cpu: 380 ms)
$chrono analysis: 198 ms (cpu: 2.92 s)
$chrono factorisation: 34.2 ms (cpu: 270 ms)
$chrono line_solve: 2.87 ms (cpu: 30 ms)
$chrono Newton iteration: 260 ms (cpu: 3.61 s)
===========================================================
NEWTON : ITERATION 3
===========================================================
|| matrix || = 1.50698e+10 5.35102e+11
|| rhsU || = 6074.64 63896.9
|| rhsL1 || = 6.98412e-20 1.8534e-19
|| rhsL2 || = 4.60425e-20 1.44538e-19
|| rhsL3 || = 1.27258e-19 4.25312e-19
|| rhsL4 || = 5.07715e-20 1.57127e-19
|| rhsL5 || = 6.24713e-20 1.83325e-19
|| rhsL6 || = 0 0
|| rhsL || = 63896.9 5.42613e-19
rhsU / rhsU0 = 0.0159787
rhsL / rhsL0 = 0.0188735
|| lhsU || = 8.18951e-05 0.00068554
|| lhsL1 || = 667.22 2699.54
|| lhsL2 || = 667.22 2699.54
|| lhsL3 || = 3973.7 15468.4
|| lhsL4 || = 667.22 2699.54
|| lhsL5 || = 667.22 2699.54
|| lhsL6 || = 3973.7 15468.4
|| lhsL || = 3973.7 22532
lhsU / lhsU0 = 0.0016379
lhsL / lhsL0 = 0.00132973
---------------- ITERATION 3 TIMES ----------------------
$chrono assembly: 22.1 ms (cpu: 310 ms)
$chrono analysis: 187 ms (cpu: 2.87 s)
$chrono factorisation: 32.5 ms (cpu: 340 ms)
$chrono line_solve: 2.57 ms (cpu: 30 ms)
$chrono Newton iteration: 246 ms (cpu: 3.57 s)
===========================================================
NEWTON : ITERATION 4
===========================================================
|| matrix || = 1.50698e+10 5.35108e+11
|| rhsU || = 17.7162 169.157
|| rhsL1 || = 5.01725e-22 1.06596e-21
|| rhsL2 || = 3.90394e-22 8.42683e-22
|| rhsL3 || = 5.18628e-22 1.45097e-21
|| rhsL4 || = 3.21889e-22 8.80422e-22
|| rhsL5 || = 6.15096e-22 1.25227e-21
|| rhsL6 || = 0 0
|| rhsL || = 169.157 2.50899e-21
rhsU / rhsU0 = 4.66006e-05
rhsL / rhsL0 = 4.99646e-05
|| lhsU || = 4.01466e-07 2.07101e-06
|| lhsL1 || = 0.667561 2.17419
|| lhsL2 || = 0.667561 2.17419
|| lhsL3 || = 6.74815 20.0344
|| lhsL4 || = 0.667561 2.17419
|| lhsL5 || = 0.667561 2.17419
|| lhsL6 || = 6.74815 20.0344
|| lhsL || = 6.74815 28.6646
lhsU / lhsU0 = 8.02932e-06
lhsL / lhsL0 = 2.25816e-06
---------------- ITERATION 4 TIMES ----------------------
$chrono assembly: 20.9 ms (cpu: 330 ms)
$chrono analysis: 186 ms (cpu: 2.94 s)
$chrono factorisation: 36 ms (cpu: 380 ms)
$chrono line_solve: 3.01 ms (cpu: 20 ms)
$chrono Newton iteration: 247 ms (cpu: 3.69 s)
===========================================================
NEWTON : ITERATION 5
===========================================================
|| matrix || = 1.50698e+10 5.35108e+11
|| rhsU || = 0.000346547 0.00230493
|| rhsL1 || = 6.47782e-25 1.25162e-24
|| rhsL2 || = 4.78813e-25 1.15123e-24
|| rhsL3 || = 2.60545e-24 4.72786e-24
|| rhsL4 || = 5.78613e-25 1.26258e-24
|| rhsL5 || = 4.96936e-25 1.21482e-24
|| rhsL6 || = 0 0
|| rhsL || = 0.00230493 5.32113e-24
rhsU / rhsU0 = 9.11557e-10
rhsL / rhsL0 = 6.80818e-10
|| lhsU || = 7.74334e-12 3.6602e-11
|| lhsL1 || = 1.19104e-05 4.03829e-05
|| lhsL2 || = 1.19141e-05 4.03825e-05
|| lhsL3 || = 9.27449e-05 0.000240208
|| lhsL4 || = 1.19127e-05 4.03839e-05
|| lhsL5 || = 1.19092e-05 4.03837e-05
|| lhsL6 || = 9.27502e-05 0.000240215
|| lhsL || = 9.27502e-05 0.00034918
lhsU / lhsU0 = 1.54867e-10
lhsL / lhsL0 = 3.10373e-11
---------------- ITERATION 5 TIMES ----------------------
$chrono assembly: 23.9 ms (cpu: 370 ms)
$chrono analysis: 191 ms (cpu: 3.01 s)
$chrono factorisation: 31.5 ms (cpu: 300 ms)
$chrono line_solve: 2.55 ms (cpu: 20 ms)
$chrono Newton iteration: 250 ms (cpu: 3.72 s)
===========================================================
NEWTON : ITERATION 6
===========================================================
|| matrix || = 1.50698e+10 5.35108e+11
|| rhsU || = 1.78916e-07 1.75552e-06
|| rhsL1 || = 6.17025e-30 1.56234e-29
|| rhsL2 || = 6.23998e-30 1.30949e-29
|| rhsL3 || = 2.38719e-29 4.46019e-29
|| rhsL4 || = 1.42536e-29 2.38857e-29
|| rhsL5 || = 1.04086e-29 1.87038e-29
|| rhsL6 || = 0 0
|| rhsL || = 1.75552e-06 5.7665e-29
rhsU / rhsU0 = 4.70619e-13
rhsL / rhsL0 = 5.18535e-13
|| lhsU || = 5.72818e-17 7.22562e-16
|| lhsL1 || = 1.13561e-08 4.10896e-08
|| lhsL2 || = 9.64226e-09 3.50239e-08
|| lhsL3 || = 1.46937e-08 5.50488e-08
|| lhsL4 || = 1.14935e-08 3.95523e-08
|| lhsL5 || = 7.79764e-09 3.12645e-08
|| lhsL6 || = 1.89176e-08 5.67205e-08
|| lhsL || = 1.89176e-08 1.08187e-07
lhsU / lhsU0 = 1.14564e-15
lhsL / lhsL0 = 6.33048e-15
---------------- ITERATION 6 TIMES ----------------------
$chrono assembly: 18 ms (cpu: 280 ms)
$chrono analysis: 191 ms (cpu: 3 s)
$chrono factorisation: 37.4 ms (cpu: 330 ms)
$chrono line_solve: 3.15 ms (cpu: 30 ms)
$chrono Newton iteration: 250 ms (cpu: 3.66 s)
===========================================================
===========================================================
===========================================================
===========================================================
===========================================================
*** Newton convergence in 6 iterations. STOP. ***
===========================================================
===========================================================
===========================================================
$chrono assembly <mean>: 22.1 ms (cpu: 340 ms)
$chrono analysis <mean>: 189 ms (cpu: 2.92 s)
$chrono factorisation <mean>: 34.8 ms (cpu: 340 ms)
$chrono line_solve <mean>: 2.79 ms (cpu: 20 ms)
$chrono update <mean>: 228 us (cpu: 0 ms)
$chrono Newton iteration <mean>: 250 ms (cpu: 3.64 s)
9 - Writing mesh solution: HyperElasticity_multimat_0_grid3