Hyperelasticity
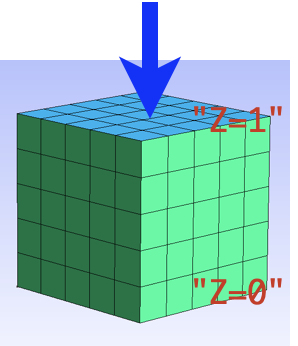
solve( Problem("Cube.msh", OptionsUP(degreeU,nGauss))
+ Hyperelasticity( hooke_E_nu(E,nu), linear=true )
& Dirichlet{
{"Z=0",2},
{"Z=1",2,-0.1}
}
, opt);
The Hyperelasticity formulator operates on all the elements by default. Should we have different materials, we would have to specify the subdomain like this:
solve (...
+ ElementFormulatorUP( Hyperelasticity(hooke1), ElementList1 )
+ ElementFormulatorUP( Hyperelasticity(signorini1),ElementList2 )
+ ElementFormulatorUP( Hyperelasticity(hooke2), ElementList3 )
Degree and integration rule
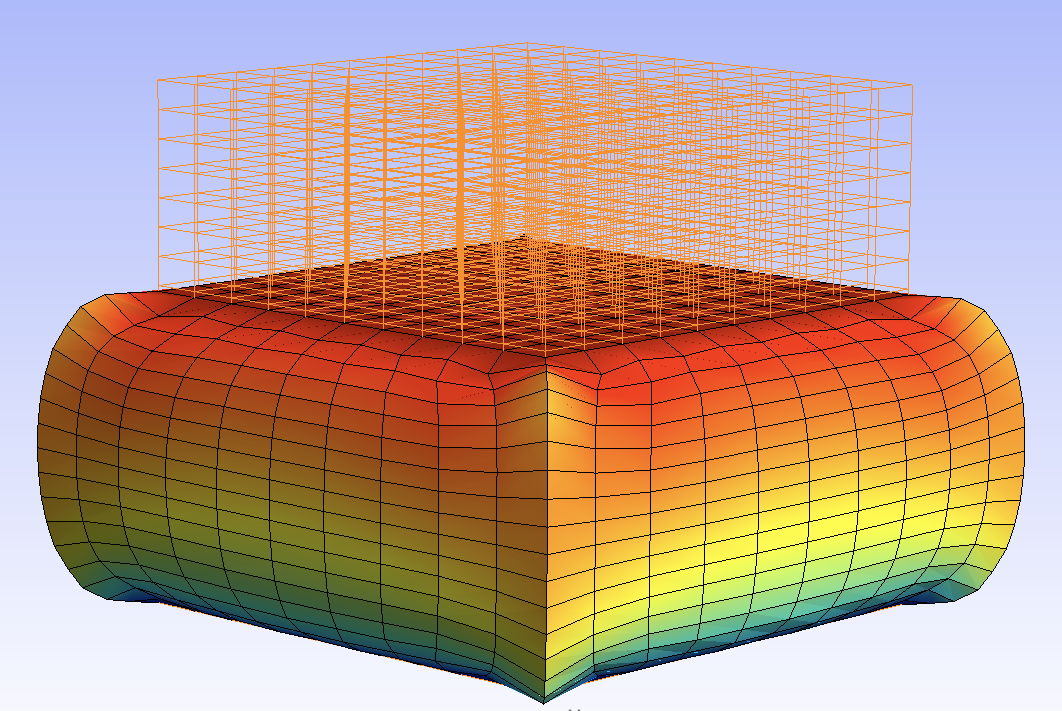
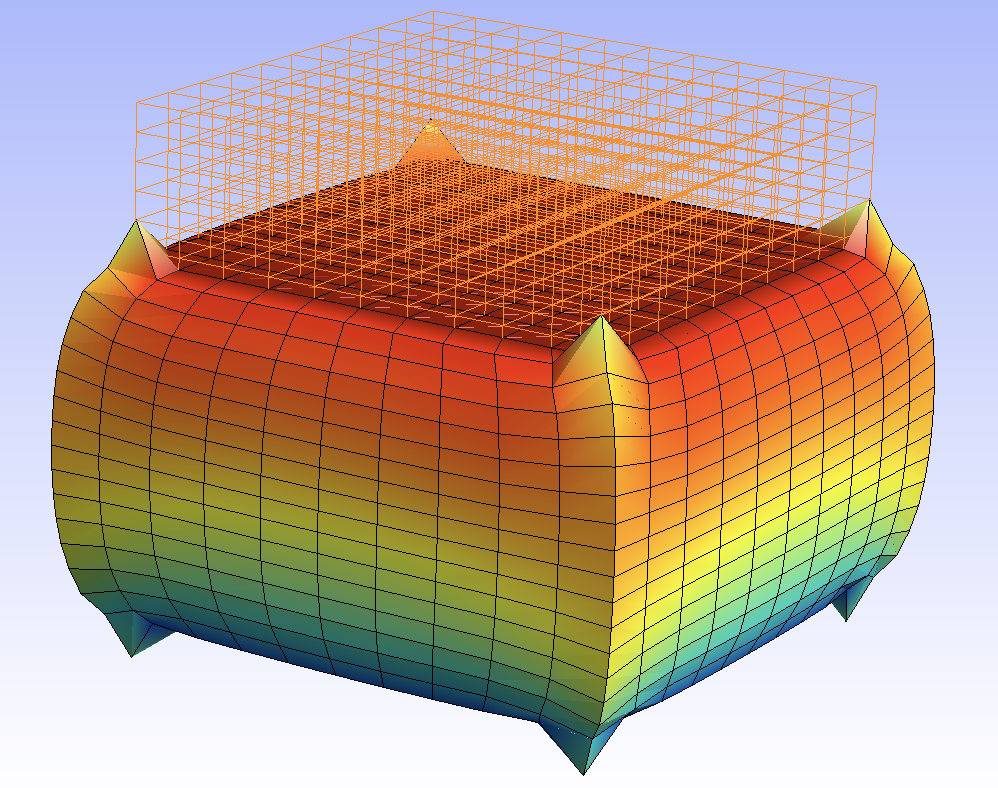
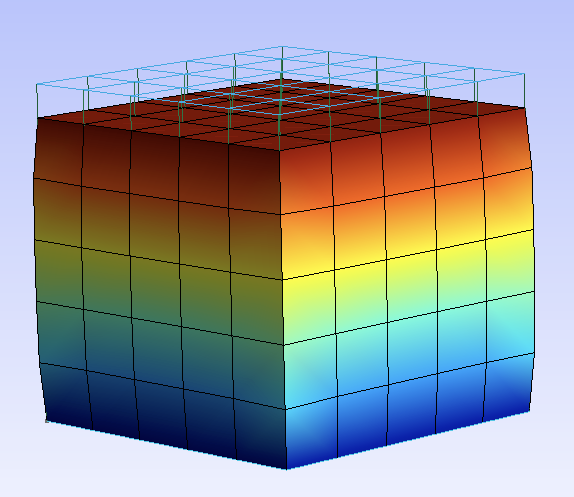
The interpolation degree is important. A higher degree can detect phenomena before lower degrees:
degree 1 |
degree 2 |
dz=-0.4 |
dz=-0.3 |
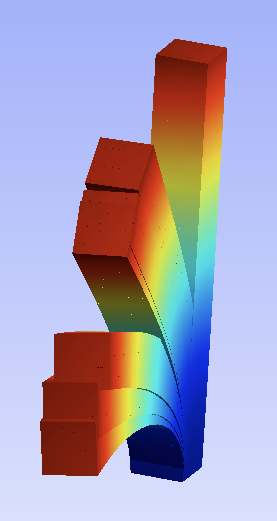
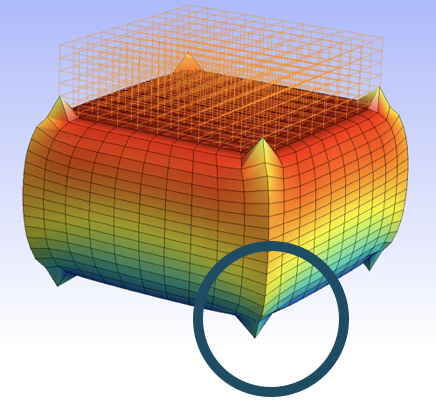
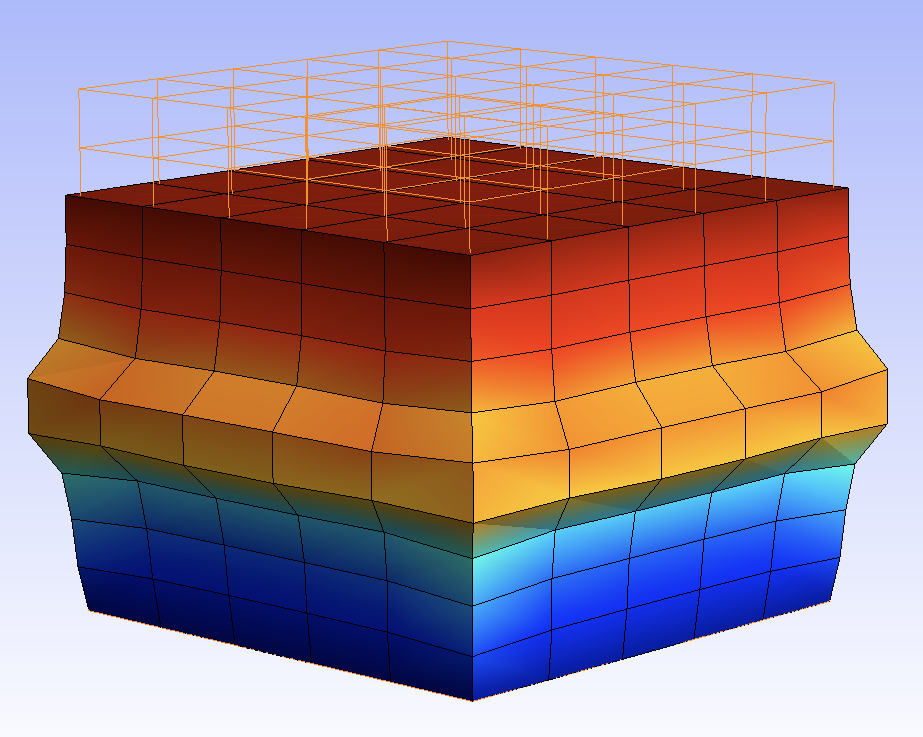
In this case the nodes on the vertical edges have undergone a severe displacement. We can guess such a behaviour when the cube is crushed with a piece of its width, that is, without retaining the nodes from going under the bottom or over the top. We’ll see later how to penalize the penettration of the nodes.
The number of Gauss point may be specified:
A volumic force
A force may apply on elements of different dimensions; we precise the relative dimension: RDIM means relative dimension equal to the space dimension.
Expr force = coef*Vector(.0,x*y,.0);
solve (...
+ ExternalForce<RDIM>(force)
As it is declared, it operates by default on the whole domain.
A surfacic force
The force applies now to sides, whose relative dimension is the dimension minus 1: RCODIM1.
+ SideFormulatorUP( ExternalForce<RCODIM1>(force), sides_extractor<Grid3>("top") )
A lineic force
The relative dimension is now 1: RDIM1. Definitely absolute, but given as a member of the relative dimensions family!
Incompressibility
This option is controlled by the Hyperelasticity formulator, but a degree for P is required:
solve( ..., OptionsUP(degreeU,degreeP,nGauss))
+ Hyperelasticity( incompressible(signorini0),kIm) & ...);
where kIm is the kind of modified invariants desired for the computation. Having a material energy \(w\), we can use:
\(w(I_1,I_2)\) with \(I_3=1\) (
kIm = Invariants::NATURAL;)\(w(\frac{I_1}{I_3^{1/3}},\frac{I_2}{I_3^{2/3}})\) (
kIm = Invariants::ISOCHORIC_MULTIPLICATIVE;)…
Rigid body attachment
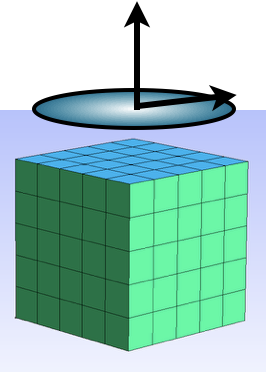
The rigid body is used to move a list of nodes together in a rigid body motion
Attach the nodes to some rigid body named « RigiBody0 ». For now, it is just a name.
solve ( ...
& NodesOnRigidBody("Z=1", "RigidBody0")
Apply a force to the rigid body:
solve ( ...
& RigidBodyForce("RigidBody0", Vector(.0,.0,-E*0.08)
or a rotation:
& RigidBodyRotation("RigidBody0", Vector(0.,0.0,2*Pi*t))
the parameter t being an constant expression in our context:
const auto t = Expr("t");
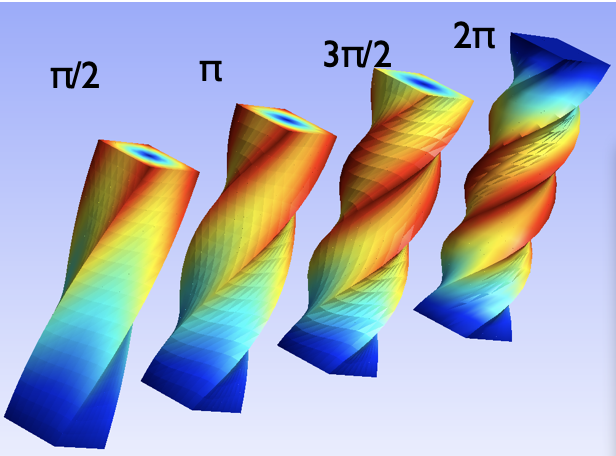
that stands for the time or pseudo time to decompose the action. It is used to apply the imposed rotation progressively, because a \(2\pi\) rotation is either huge … or not! For this, we only add option Times to the problem:
solve( Problem(...,Times(4))) ...
meaning a split between 4 equal parts for the time duration set by default to 1. The first value is 0, standing for the starting point. An array of specific time values could be given as well.
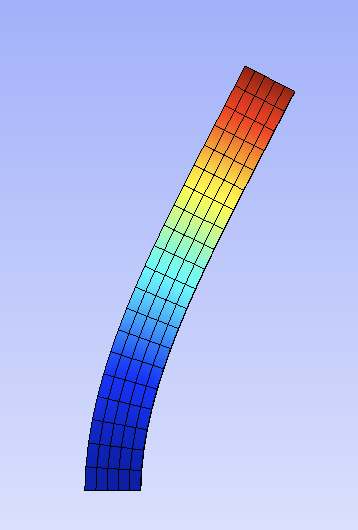
Here the solver was asked to solve in 4 steps the torsion case:
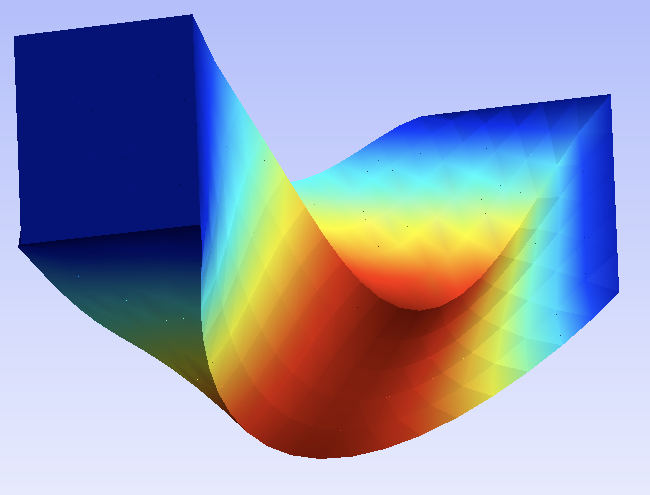
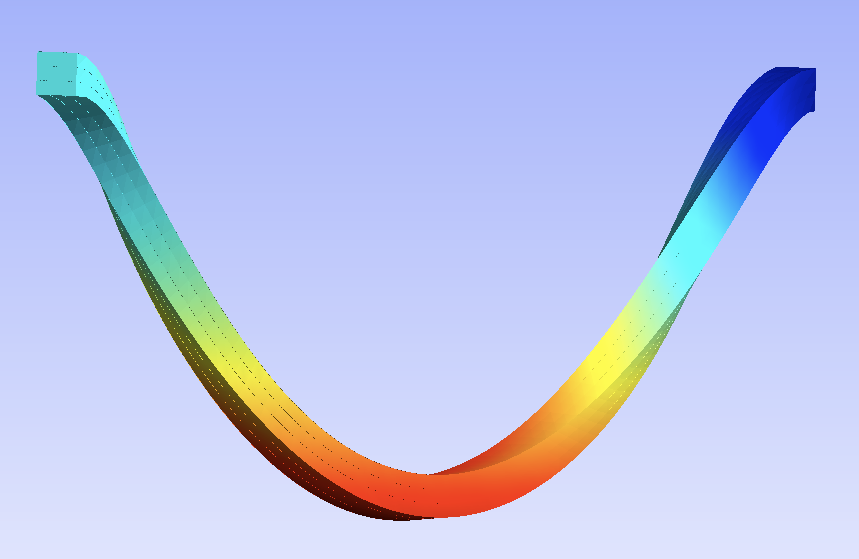
Penalization on nodes displacement for rigid contact
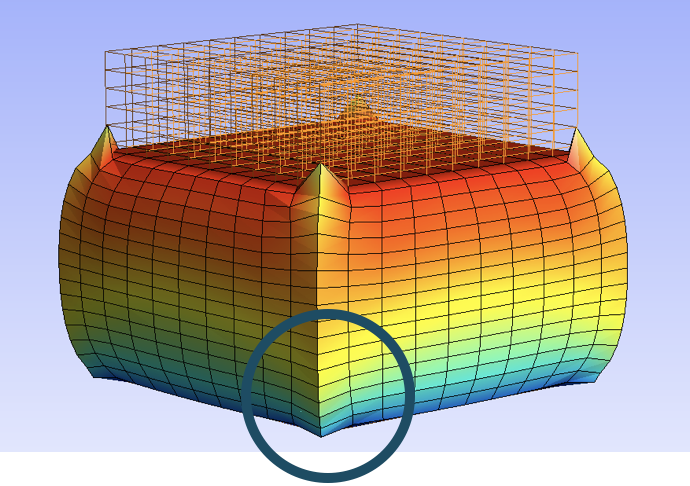
With a severe crush of the cube, some nodes on the vertical edges come under the sole level (z=0.). To overcome this, we penalize their penetration. The node formulator is built in-line; it requires the derivative of the penalization function:
Let \(K^- = \left\{ \begin{array}{l} 0 \text{ if } z+u_z\ge0;\\ K \text{ otherwise.} \end{array}\right.\;\;\;\) Then the functions write: \(\left\{\begin{array}{rcll}w &=& \frac{1}{2} &K^-(z+u_z)^2\\ \frac{\partial w}{\partial u}&=& &K^-(z+u_z)\;e_z\\\frac{\partial^2 w}{\partial u^2} &=& &K^-\;e_z\otimes e_z\end{array}\right.\)
Expr eZ = vector_cast(0.,0.,1.);
Expr K = 1.e6;
Expr Kn = select( test_ge0(z+uz), 0., K);
solve(...
+ NodeFormulatorUP( "Z=0"
, .5 * Kn * pow(z+uz,2)
, Kn * (z+uz)*eZ
, Kn * tensorial(eZ,eZ))
without penalization |
with penalization |