Simulation numérique et dérivation automatique

En vue de l’optimisation d’un système régi par un modèle numérique, il est pertinent de vouloir accéder aux sensibilités de son état vis-à-vis de ses paramètres, comme les coefficients des lois physiques, les paramètres géométriques, ou les coefficients de chargement. Les sensibilités, recherchées par les concepteurs, sont les variations linéarisées de l’état en fonction des paramètres. De façon plus ciblée, on veut accéder aux sensibilités des critères à optimiser, c’est-à-dire à leurs gradients dans l’espace des paramètres de conception.

À partir d’un code de simulation

Quant on dispose d’un code source de simulation numérique, il est naturel de le faire évoluer afin de lui faire produire les sensibilités recherchées.

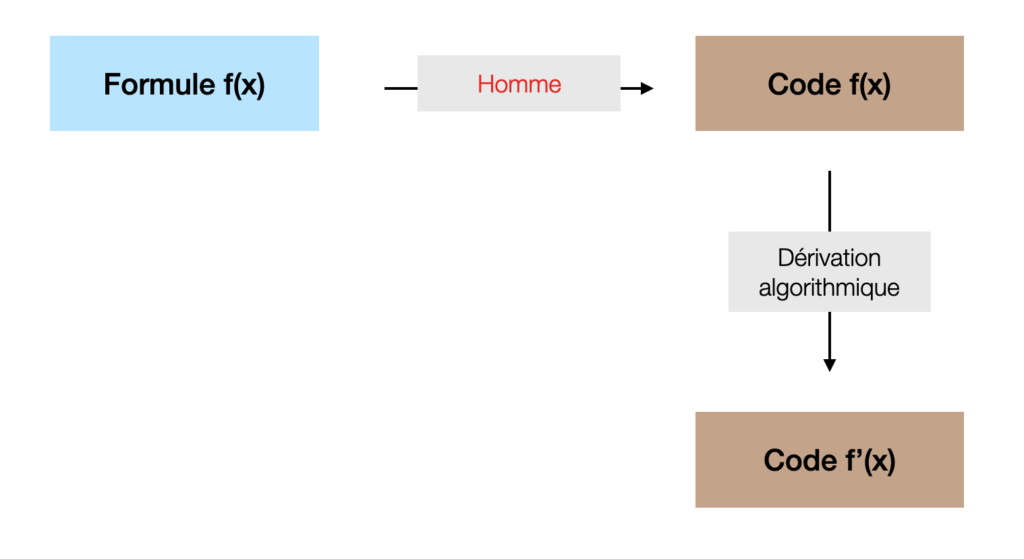
Depuis les années 80, des équipes de recherche ont mis au point des logiciels capables de générer le code donnant la dérivée à partir de celui d’origine. Les codes écrits en Fortran en ont été les premiers bénéficiaires, pour la double raison de l’absence de pointeurs et de leur part très importante des logiciels de simulation. Depuis environ l’an 2000, on a vu l’essor du C++ dans la simulation et son traitement par les logiciels de différentiation source-à-source. Une technique consiste à profiter dans le langage C++ de la surcharge des fonctions et des opérateurs, ce qui réduit la charge de la participation humaine.

Le principe de la dérivation ligne-à-ligne est simple; il s’agit une dérivation formelle opérant sur les instructions et les variables élémentaires d’un programme informatique. D’autre part, la complexité est maîtrisée: il est prouvé que le résultat requiert un nombre d’opérations du même ordre de grandeur que le calcul initial. Cependant, parmi les difficultés, on recense le traitement de la mémoire, les fonctions implicites résolues par une boucle itérative de point fixe, le parallélisme des instructions, le choix entre mode direct et mode adjoint ou inverse. Enfin, la nécessité d’une certaine assistance humaine en fait plutôt une méthode semi-automatique.

Cependant, malgré les qualités de la différentiation algorithmique, la connaissance du modèle mathématique doit théoriquement aider à produire un meilleur code.

À partir d’une formule mathématique

Idéalement, le développeur suit un modèle formulé mathématiquement pour le programmer. En dérivant sa formule, il peut en programmer le résultat. Ainsi, une dérivation automatique à partir d’une formule exige non seulement un mécanisme de dérivation symbolique mais aussi une traduction de la formule en fonction de calcul écrite en un programme informatique.

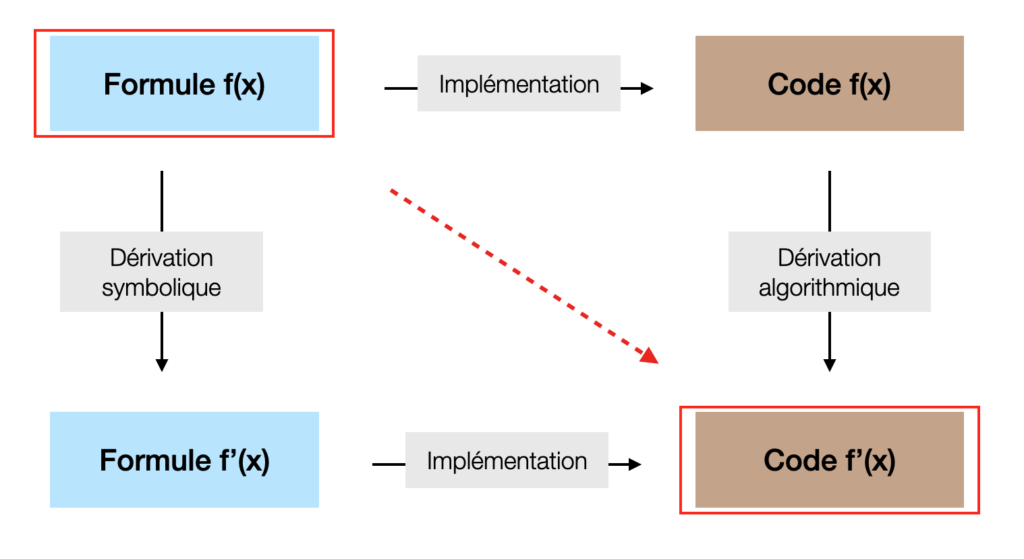
La dérivation symbolique opère sur des expressions et des objets informatiques représentant des valeurs ou des variables mathématiques de différentes complexités.

Les modes direct et adjoint mentionnés plus haut ne sont pas des notions de la dérivation symbolique: la dérivée est une expression sans égard à son calcul par la gauche ou la droite. Un automate adoptera ensuite une façon optimale (heuristiquement parlant) de chaîner les produits matriciels issus de la dérivation, ou plus précisément de ceux qui restent après simplification.

Le travail “symbolique” consiste à analyser et manipuler des expressions algébriques et doit considérer sérieusement la tâche de simplification. La dérivation multipliant le nombre de termes, il est important de savoir les recombiner pour alléger au maximum le résultat et atteindre l’efficacité exigée par les calculs intensifs de la simulation numérique.

Sur le schéma, ce qu’on nomme implémentation et code doivent s’entendre de manière très abstraite. En effet, comme on ne part plus d’un code source existant, le code résultant n’est plus obligatoirement un autre code source mais peut être une chaîne de calcul interne ou bien encore une formule et un interpréteur de formule.

Traduction de formule en fonction de calcul

Plusieurs options se présentent. Soit la formule est interprétée, c’est-à-dire que l’arbre d’expressions est parcouru à la volée et calculé en le remontant, de façon interne, sans sortir du programme d’exécution.

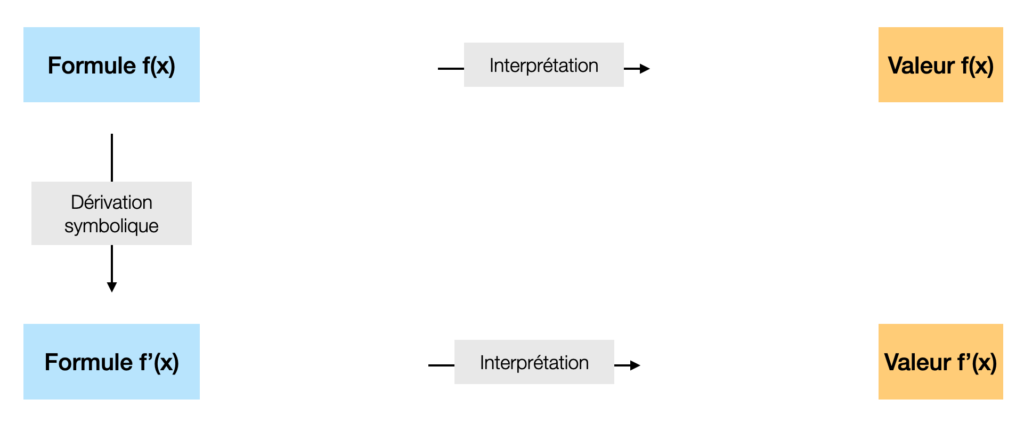
Soit la formule est d’abord analysée pour former un arbre d’appel, qui peut être soit traduit en un code écrit dont le résultat de la compilation sera adjoint au binaire exécutable, soit parcouru à l’exécution à la condition que les fonctions figurent déjà dans l’exécutable. Le cas de l’interpréteur en est un cas particulier, pour lequel la formule est évaluée telle quelle, à la volée. Retenons que cette étape de préparation laisse des possibilités d’optimisation qui seront appréciées pour des formules réévaluées après une mise-à-jour de ses paramètres: la chaîne n’est alors pas reconstruite, seules les valeurs des données sur lesquelles elle travaille ont changé.

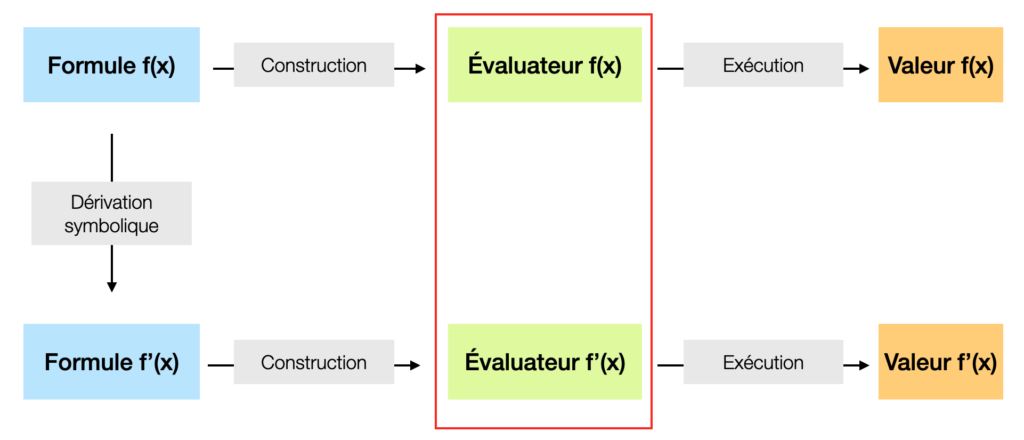
La formation d’un arbre d’appel peut sans difficulté être adaptée à plusieurs formules qui partageront éventuellement des sous-formules.

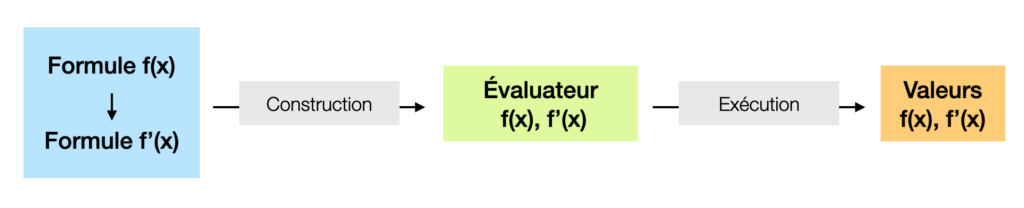
Le choix de Navpactos s’est porté sur la génération interne d’un évaluateur de formules.

Choix d’un type de dérivation

Celui-ci va dépendre de l’origine de l’objet à dériver.

• À partir d’un exécutable en boîte noire: seule la différence finie est envisageable, ou bien …, jouissant du droit de désassemblage, la différentiation algorithmique de code assembleur!
• À partir des fonctions en boîte noire des calculs de second membre et de la matrice: la méthode semi-analytique, c’est-à-dire une différence finie sur le second membre autour de l’état préalablement calculé, puis une résolution du système linéaire avec la matrice obtenue lors du calcul de l’état.
• À partir d’un code source: la dérivation de code source, dite algorithmique. Le choix entre mode direct et mode adjoint dépend du degré de dérivation et du nombre de paramètres.
• À partir d’un modèle défini symboliquement, dans un cadre manipulant de tels modèles symboliques: la dérivation symbolique, avec la souplesse de la manipulation des modèles et des formules. L’analyse doit permettre de décider automatiquement l’utilité du calcul d’un état adjoint.
• À partir de rien: modéliser avec Navpactos et passer au point précédent!