Numerical simulation and automatic differentiation

With a view to optimizing a system governed by a numerical model, it is relevant to access the sensitivities of its state with respect to its parameters, such as the coefficients of the physical laws, the geometric parameters, or the load coefficients. The sensitivities sought by the designers are the linearized variations of the state as a function of the parameters. In a more targeted manner, the sensitivities of the criteria, often refferred as cost-functions, to be optimized, i.e. their gradients in the design parameter space, are to be accessed.

From a simulation code source

When you have a numerical simulation source code, it is natural to evolve it to produce the desired sensitivities.

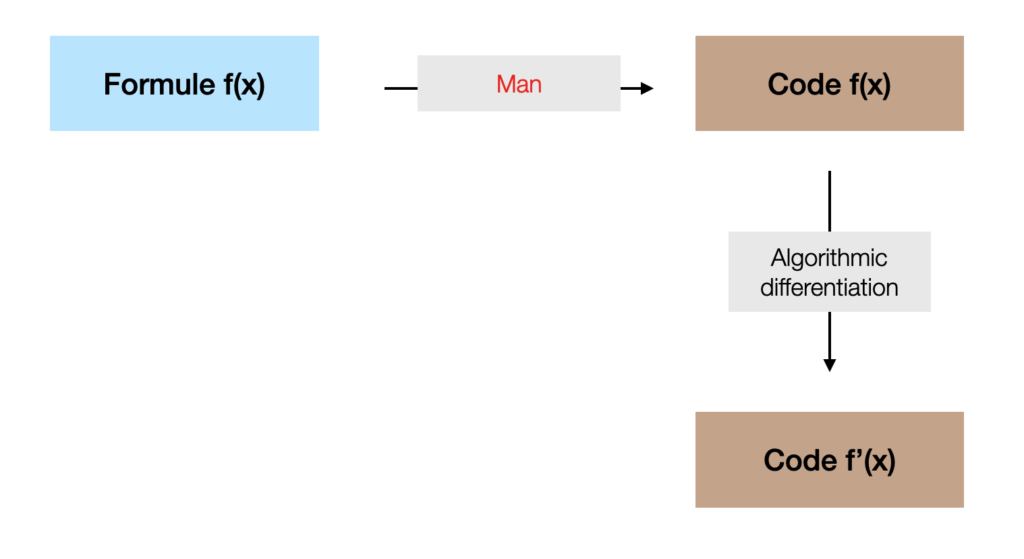
Since the 1980’s, research teams have developed software capable of generating the code giving the derivative from the original one. The codes written in Fortran were the first beneficiaries, for the two reasons of the absence of pointers and their very important part of simulation software. Since about the year 2000, C++ has been gaining momentum in simulation and its treatment by source-to-source differentiation software. One technique is to take advantage in C++ language of the overloading of functions and operators, which reduces the burden of human participation.

The principle of line-to-line derivation is simple; it is a formal derivation operating on the instructions and elementary variables of a computer program. On the other hand, complexity is controlled: it is proven that the result requires a number of operations of the same order of magnitude as the initial calculation. However, among the difficulties, there are the processing of the memory, the implicit functions resolved by an iterative fixed point loop, the parallelism of the instructions, the choice between direct mode and assistant or inverse mode. Finally, the need for some human assistance makes it more of a semi-automatic method.

However, despite the qualities of algorithmic differentiation, knowledge of the mathematical model should theoretically help produce better code.

From a mathematical formula

Ideally, the developer follows a mathematically formulated model to program it. By deriving his formula, he can program the result. For example, automatic differentiation from a formula requires not only a symbolic differentiation mechanism but also translation of the formula to a function written as a computer program.

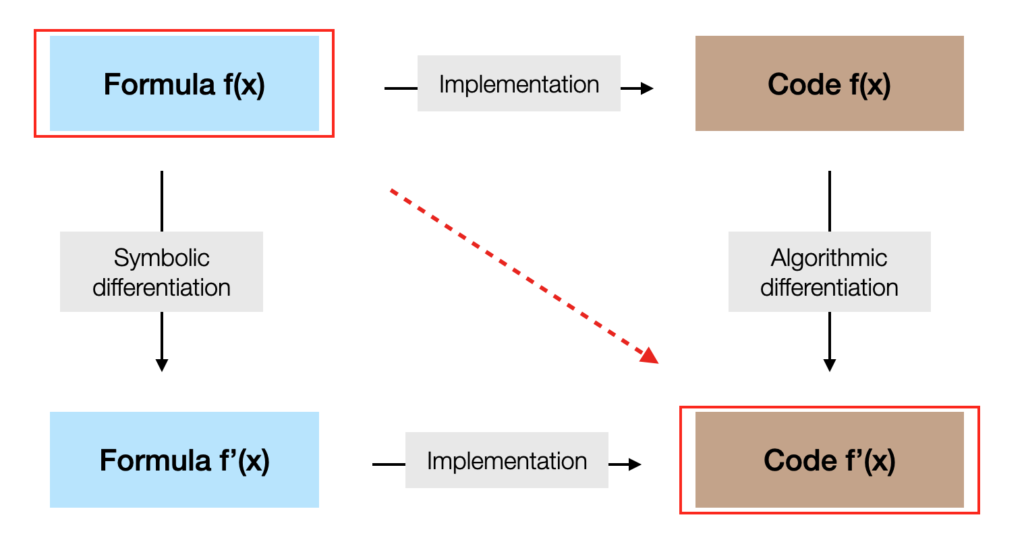
Symbolic differentiation operates on expressions and computer objects representing mathematical values or variables of different complexities.

The direct and adjoint modes mentioned above are not notions of symbolic differentiation: the derivative is an expression without regard to its calculation by the left or the right. An automaton will then adopt an optimal (heuristically speaking) way of chaining the matrix products resulting from the differentiation, or more precisely those which remain after simplification.

“Symbolic” work consists in analyzing and manipulating algebraic expressions and must seriously consider the task of simplification. Since differentiation multiplies the number of terms, it is important to know how to recombine them to reduce the result to the maximum and achieve the efficiency required by the intensive computations of the numerical simulation.

On the diagram, what is called implementation and code must be understood in a very abstract manner. Indeed, since the starting point is no longer an existing source code, the resulting code is no longer necessarily another source code but may be an internal calculation chain or else a formula with a formula interpreter.

Formula translation based on calculation

There are several options. Either the formula is interpreted, i.e. the expression tree is traversed on the fly and calculated bottom-up internally without leaving the execution program.

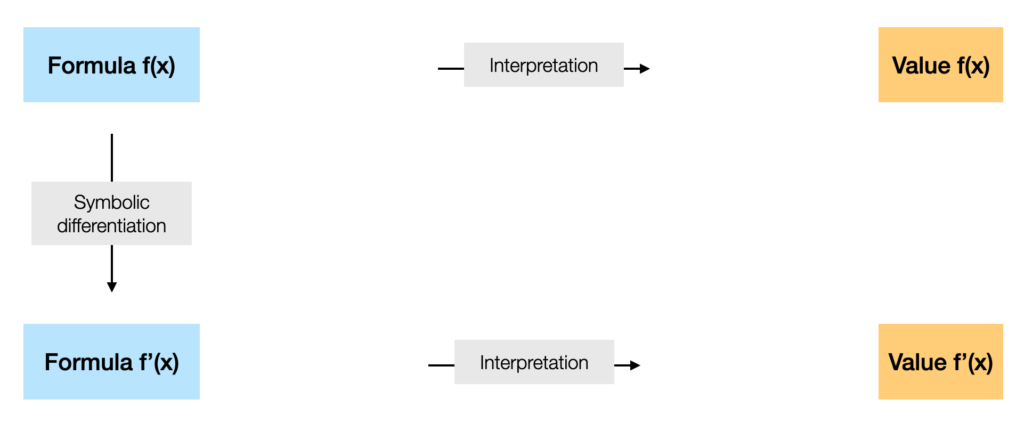
Either the formula is first parsed to form a call tree, which can either be translated into written code whose compilation result will be appended to the executable binary, or run through the execution on the condition that the functions are already in the executable. The case of the interpreter is a particular case, for which the formula is evaluated as it is, on the fly. Let us remember that this preparation step leaves possibilities of optimization which will be appreciated for formulas reevaluated after an update of its parameters: the chain is then not reconstructed, only the values of the data on which it works have changed.

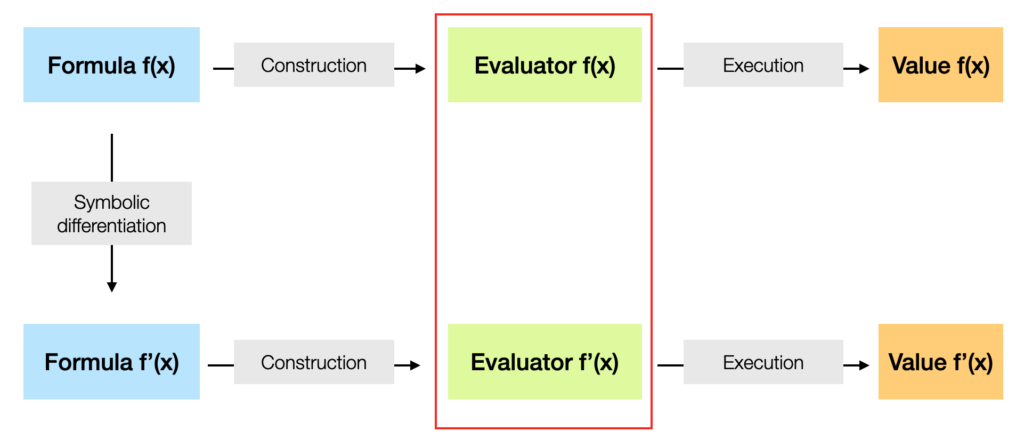
The formation of a call tree can easily be adapted to several formulas which will eventually share subformulas.

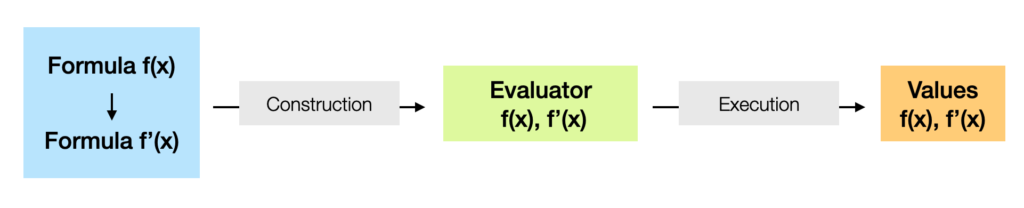
The choice of Navpactos focused on the internal generation of a formula evaluator.

Choosing a differentiation method

This will depend on the origin of the object to be differentiated.

• From a black box executable: only the finite difference method is conceivable, or else, enjoying the right of disassembly, the algorithmic differentiation of assembler code!
• From the black box functions of the calculations of the second member and of the matrix: the semi-analytical method, that is to say a finite difference on the second member around the previously calculated state, then a resolution of the linear system with the matrix obtained during the calculation of the state.
• From a source code: the differentiation of source code, called algorithmic. The choice between direct mode and auxiliary mode depends on the degree of derivation and the number of parameters.
• From a symbolically defined model, in a framework manipulating such symbolic models: symbolic differentiation, with the flexibility of manipulation of models and formulas. The analysis should automatically decide the usefulness of calculating an adjoint state.
• From scratch: model with Navpactos and go to the previous point!