Naupacte was present with a speaker at the SIA 2023 Congress in numerical simulation, during a Data & Optimization session. This was an opportunity to show what can be expected in terms of computational automation when one embarks on non-linear multiphysics modeling and simulation.
Automation of calculations
Automation of calculations leads to optimization of
- the application developer,
- the execution of calculations,
- as well as the object studied, thanks to the optimal design algorithms.
The developer formulates its multiphysical coupling, while Navpactos takes care of the rest, i.e. the construction of the matrix and the second member obtained by assembly of finite elements. It is even sufficient to specify the construction of the second member, if one wants the tangent matrix, because it is deduced therefrom by derivation … with respect to the degrees of freedom. Navpactos takes care of everything.
Navpactos even takes care of more: examples of optimization in order 2, that is to say based on the Jacobian of the optimality equations, i.e. the Hessian of the Lagrangian, have been shown. With respect to the programming of the direct problem, it is sufficient to specify the parameters to be optimized and to formulate the cost function to be minimized. Everything else is automatic, which includes a differentiation of the tangent matrix! And also a linear search replaced by a search on a parabolic arc osculating the state curve.
Case Study and Convergence
The case shown was derived from non-linear elasticity with the two coefficients of the polynomial giving the imposed displacements on a face as parameters.
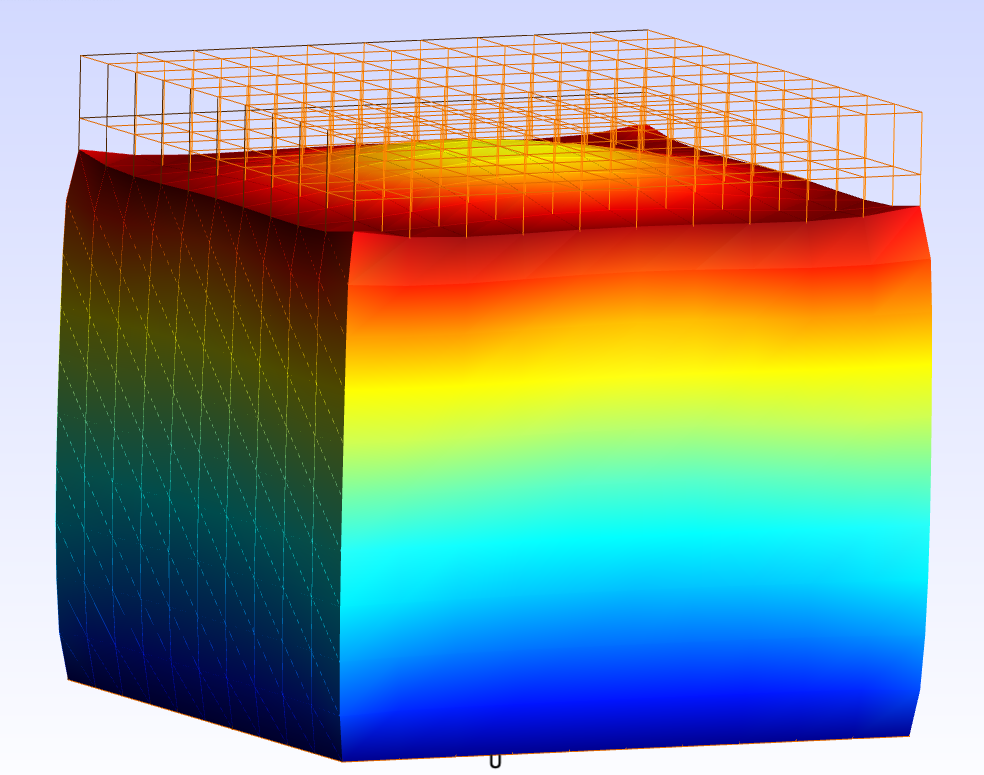
Example judiciously chosen (ah! chance) because it illustrates a consequence of poor conditioning: the direction of descent estimated by the hessian almost orthogonal to the gradient. The gain in iterations is colossal compared with a method of steepest descent.
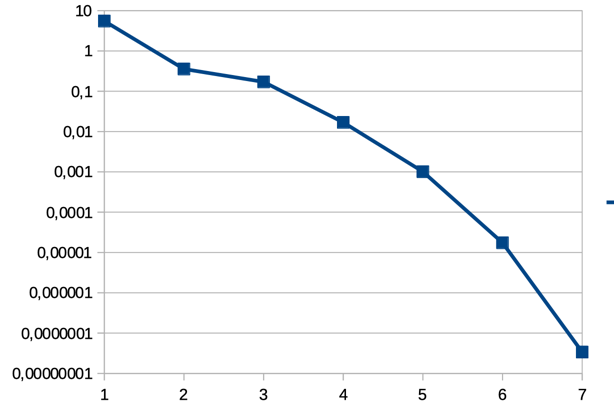
The convergence of the residue of the gradient in the parameter space is very fast. This is a favorable case: an inverse problem where the cost function measures the difference on results with those of target parameters. This type of case validates the calculation of the derivatives a posteriori.
